1.Trên nửa đường kính AB,lấy hai điểm P,Q sao cho P thuộc cung AQ.Gọi C là giao điểm của tia BQ;H là giao điểm của dây cung AQ và BP
a)Chứng minh tứ giác CPHQ nội tiết đường tròn
b) Chứng minh ∆ CBP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc APB=góc AQB=1/2*180=90 độ
=>AQ vuông góc BC, BP vuông góc CA
góc CPH+góc CQH=180 độ
=>CPHQ nội tiếp

a) Vì AB là đường kính \(\Rightarrow\angle ACB=\angle ADB=90\Rightarrow ECHD\) nội tiếp
b) ECHD nội tiếp \(\Rightarrow\angle CEH=\angle CDH=\angle CDA=\angle CBA\)
Xét \(\Delta CEH\) và \(\Delta CBA:\) Ta có: \(\left\{{}\begin{matrix}\angle CEH=\angle CBA\\\angle ECH=\angle BCA=90\end{matrix}\right.\)
\(\Rightarrow\Delta CEH\sim\Delta CBA\left(g-g\right)\Rightarrow\dfrac{CE}{HC}=\dfrac{BC}{AC}\Rightarrow CE.AC=BC.HC\)
a, xét nửa đường tròn đường kính AB
có tam giác ABD nội tiếp => góc ADE=90 độ
có tam giác ABC nội tiếp=> góc BCE=90 độ
=>góc ADE+góc BCE=180 độ
mà 2 góc này đối diện=>tứ giác ECHD nội tiếp
b, xét tam giác ADE và tam giác BCE có
góc E chung, góc ADE= góc BCE(cmt)
=>tam giác ADE đồng dạng tam giác BCE(g.g)
=>\(\dfrac{ED}{EC}=\dfrac{AD}{BC}< =>\dfrac{EC}{BC}=\dfrac{ED}{AD}\)(1)
xét tam giác ACH và tam giác ADE có
góc A chung, góc ACH= góc ADE(=90 độ)
=>tam giác ACH đồng dạng tam giác ADE(g.g)
=>\(\dfrac{AC}{AD}=\dfrac{HC}{DE}\)<=>\(\dfrac{ED}{AD}=\dfrac{HC}{AC}\left(2\right)\)
từ(1)(2)=>\(\dfrac{HC}{AC}=\dfrac{EC}{BC}=>EC.AC=HC.BC\left(dpcm\right)\)

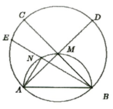
Các tam giác ∆ANE, ∆AMC và ∆BMD vuông cân
=> A E B ^ = A D B ^ = A C B ^ = 45 0
Mà AB cố định nên các điểm A, B, C, D, E cùng thuộc một đường tròn