help với thanks mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2021
Bài 4:
a: \(x\in\left\{28;42;56;70\right\}\)
b: x=10
10 tháng 8 2016
Để \(\frac{4n+3}{3n+1}\) thuộc Z thì 4n + 3 chia hết cho 3n + 1
\(\Rightarrow3\left(4n+3\right)⋮3n+1\)
\(\Rightarrow12n+9⋮3n+1\)
\(\Rightarrow\left(12n+4\right)+5⋮3n+1\)
\(\Rightarrow4\left(3n+1\right)+5⋮3n+1\)
\(\Rightarrow5⋮3n+1\)
\(\Rightarrow3n+1\in\left\{\pm1;\pm5\right\}\)
+) 3n + 1 = 1\(\Rightarrow n=0\) ( chọn )
+) \(3n+1=-1\Rightarrow n=\frac{-2}{3}\) ( loại )
+) \(3n+1=5\Rightarrow n=\frac{4}{3}\) ( loại )
+) \(3n+1=-5\Rightarrow n=-2\)
Vậy n = 0 hoặc n = -2
I3
23 tháng 11 2021
ƯC của(−15;+20) là: {±1;±5}
đây là theo hiểu biết của mk thôi nha, ko chép ai đâu^^
PA
12 tháng 7 2016
Ox và Ox' là 2 tia đối nhau
=> xOx' = 1800
Oy và Oy' là 2 tia đối nhau
=> yOy' = 1800
\(xOx'+3\times yOx'=240^0\)
\(180^0+3\times yOx'=240^0\)
\(3\times yOx'=240^0-180^0\)
\(3\times yOx'=60^0\)
\(yOx'=\frac{60^0}{3}\)
\(yOx'=20^0\)
mà y'Ox = yOx'
=> y'Ox = 200
CC
1
11 tháng 10 2021
Khi chia 2021 số bất kỳ cho 2020 ta sẽ có mỗi số có một số dư trong 2020 số dư: 0, 1, 2,…, 2020. Do đó theo nguyên lý Dirichlet phải tồn tại ít nhất hai số có cùng số dư. Hiệu của hai số đó sẽ chia hết cho 2020.
CC
2
NA
10 tháng 11 2021
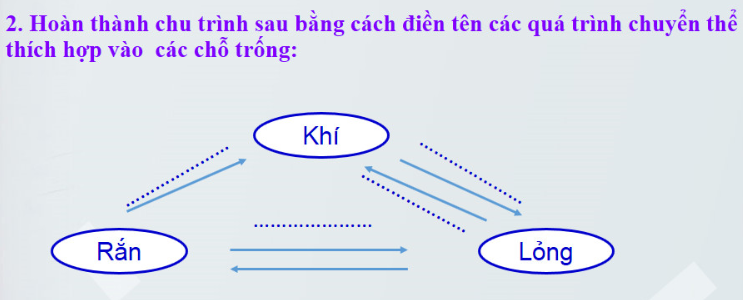
Lỏng -> Khí : Khi mở lọ nước hoa , mùi bay
Lỏng -> Rắn : Khi bỏ nước vào tủ lạnh và đông đá
CC
1
10 tháng 10 2021
a) \(\Rightarrow\left(n+2\right)+3⋮\left(n+2\right)\)
\(\Rightarrow\left(n+2\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow n\in\left\{-5;-3;-1;1\right\}\)
b) \(\Rightarrow\left(n+1\right)+6⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
\(\Rightarrow n\in\left\{-7;-4;-3;-2;0;1;2;5\right\}\)
c) \(\Rightarrow\left(n+1\right)^2-\left(n+1\right)+13⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
\(\Rightarrow n\in\left\{-14;-2;0;12\right\}\)
d) \(\Rightarrow\left(n+2\right)^2-\left(n+2\right)+7⋮\left(n+2\right)\)
\(\Rightarrow\left(n+2\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow n\in\left\{-9;-3;-1;5\right\}\)
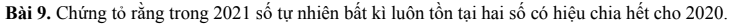
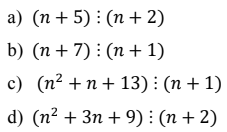
Đặt \(d=\left(16n+3,12n+2\right)\)
Suy ra
\(\hept{\begin{cases}16n+3⋮d\\12n+2⋮d\end{cases}}\Rightarrow3\left(16n+3\right)-4\left(12n+2\right)=1⋮d\Rightarrow d=1\)
Suy ra đpcm.