Trung điểm là gì
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
18 tháng 9 2017
Trung điểm là điểm cách đều 2 mút của đoạn thẳng.
Trung trực là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với mó .
Trung tuyến là đoạn thẳng nối từ đỉnh xuống trung điểm cạch đối diện .
Trong hình học phẳng, trung đoạn là đoạn thẳng vuông góc , vạch từ tâm của 1 đa giác đều xuống cạnh của nó .
18 tháng 9 2017
Trung điểm là điểm nằm chính giữa đoạn thẳng, chia đoạn thẳng ra làm hai đoạn dài bằng nhau.
Trong hình học phẳng, "trung đoạn" là đoạn thẳng vuông góc vạch từ tâm của một đa giác đều xuống cạnh của nó. Tương tự trong hình học không gian, nó là đoạn thẳng hạ từ đỉnh của một hình chóp đều xuống cạnh của đa giác đáy đó bạn.
Đường trung trực của đoạn thẳng là 1 đường thẳng vuông góc với đoạn thẳng và đi qua trung điểm của đoạn thẳng đó
Trong hình học, trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện
BW
17 tháng 12 2017
Tuyết ơi mày có câu dễ thế mà ko trả lờ được lên lớp tao phô chúng nó nha
Từ đã tao à ngườ kết bạn với mày
25 tháng 2 2023
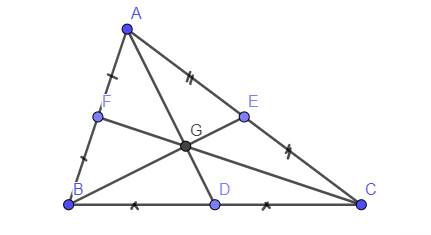
`+,` Có `D` là trung điểm của `BC(GT)`
`=>AD` là trung tuyến của `Delta ABC`
`+,` Có `BE` là trung tuyến của `Delta ABC`
`CF` là trung tuyến của `Delta ABC`
mà `BE` cắt `CF` tại `G`
nên `G` là trọng tâm của `Delta ABC`
+, Có `AD` là trung tuyến của `Delta ABC(cmt)`
mà `G` là trọng tâm của `Delta ABC`
nên `G in AD`
`=>A;D;G` thẳng hàng ( đpcm )
KH
12 tháng 5 2017
1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.
KH
12 tháng 5 2017
1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.
17 tháng 10 2021
a, Vì D,E là trung điểm AB,AC nên DE là đtb tg ABC
Do đó \(DE=\dfrac{1}{2}BC;DE//BC\)
Vậy BDEC là hình thang
b, Vì \(DE=\dfrac{1}{2}BC\) nên \(DE=BM\left(=\dfrac{1}{2}BC\right)\)(do M là trung điểm BC)
Mà DE//BC nên DE//BM
Do đó BDEM là hình bình hành
6 tháng 11 2023
a: Xét ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét tứ giác AMBE có
D là trung điểm chung của AB và ME
=>AMBE là hình bình hành
Hình bình hành AMBE có MA=MB
nên AMBE là hình thoi
=>AE//MB và AE=MB
AE//MB
M\(\in\)BC
Do đó: AE//MC
AE=MB
MB=MC
Do đó: AE=MC
Xét tứ giác ACME có
AE//MC
AE=MC
Do đó: ACME là hình bình hành
b: Hình thoi AEBM trở thành hình vuông khi \(\widehat{MBE}=90^0\)
=>\(\widehat{MBA}=\dfrac{90^0}{2}=45^0\)
=>\(\widehat{ABC}=45^0\)
18 tháng 10 2021
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Trung điểm là điểm nằm chính giữa đoạn thẳng, chia đoạn thẳng ra làm hai đoạn dài bằng nhau. Công thức để xác định trung điểm của một đoạn thẳng trên một mặt phẳng.
là điểm ở giữa hai đường thẳng và chia làm 2 phần bằng nhau(chắc thế)