Giải pt
18x3 + 12x2 -6x + 1 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
2
13 tháng 7 2021
1.
\(\left(12x^2+6x\right)\left(y+z\right)+\left(12x^2+6x\right)\left(y-z\right)\\ =\left(12x^2+6x\right)\left(y+z+y-z\right)\\ =2y\left(12x^2+6x\right)\\ =2y.6x\left(2x+1\right)\\ =12xy\left(2x+1\right)\)
2.
\(x\left(x-6\right)+10\left(x-6\right)=0\\ \Leftrightarrow\left(x-6\right)\left(x+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)
Vậy \(x\in\left\{6;-10\right\}\) là nghiệm của pt
13 tháng 7 2021
Bài 1:
Ta có: \(\left(12x^2+6x\right)\left(y+z\right)+\left(12x^2+6x\right)\left(y-z\right)\)
\(=\left(12x^2+6x\right)\left(y+z+y-z\right)\)
\(=6x\left(2x+1\right)\cdot2y\)
\(=12xy\left(2x+1\right)\)
Bài 2:
Ta có: \(x\left(x-6\right)+10\left(x-6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)
6 tháng 9 2017
\(8x^3+12x^2+6x+1=0\)
\(\Leftrightarrow\left(2x\right)^3+3.\left(2x\right)^2.1+3.2x.1^2+1^3\)
\(\Leftrightarrow\left(2x+1\right)^3=0\)
\(\Leftrightarrow2x+1=0\)
\(\Leftrightarrow2x=-1\Leftrightarrow x=-\dfrac{1}{2}\)
6 tháng 9 2017
đề sai, mk sửa :
\(8x^3+12x^2+6x+1=0\)
\(\Leftrightarrow\left(2x+1\right)^3=0\)
\(\Leftrightarrow2x+1=0\)
\(\Leftrightarrow2x=-1\)
\(\Leftrightarrow x=\dfrac{-1}{2}\)
Vậy ...
CM
16 tháng 12 2019
a) ĐKXĐ : 3 – 4x ≠ 0 và 3 + 4x ≠ 0 (16x2 – 9 = - (3 – 4x)(3 + 4x) ≠ 0)
⇔ x ≠ 3/4 và x ≠ -3/4
Quy đồng mẫu thức :
Khử mẫu, ta được :
-12x2 – 30x + 21 – (9x + 12x2 – 21 – 28x) = 18x – 24x2 + 15 – 20x
⇔ -12x2 – 30x + 21 – 9x – 12x2 + 21 + 28x = 18x – 24x2 + 15 – 20x
⇔ -9x = -27 ⇔ x = 3 (thỏa mãn ĐKXĐ)
Tập nghiệm : S = {3}
b) (x + 3)2 - (x -3)2 = 6x + 18
⇔ x2 + 6x + 9 – x2 + 6x – 9 = 6x + 18
⇔ 6x = 18 ⇔ x = 3
Tập nghiệm : S = {3}
CM
7 tháng 7 2019
Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm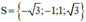 
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
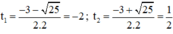
t 1 = - 2 < 0 nên loại.
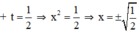
Vậy phương trình có tập nghiệm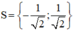 
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
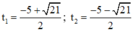
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
PT
1
CM
23 tháng 7 2019
Cả ba phương trình trên đều là phương trình trùng phương.
3x4 – 12x2 + 9 = 0 (1)
Đặt x2 = t, t ≥ 0.
(1) trở thành: 3t2 – 12t + 9 = 0 (2)
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1 và t2 = 3.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x2 = 3 ⇒ x = ±√3.
+ t = 1 ⇒ x2 = 1 ⇒ x = ±1.
Vậy phương trình có tập nghiệm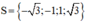 
14 tháng 11 2021
a) (x-4)(x+4)-x(x+2)=0
x2-16-x2-2x = 0
-16 - 2x = 0
2x = -16
x = -16/2
x = -8
b) 3x(x-2)-x+2=0
(3x-1)(x-2)=0
=> x ∈ {1/3 ; 2 }
c) 6x - 12x2 = 0
6x(1-2x) = 0
=> x ∈ {0; 1/2 }
d) mình thấy có vẻ hơi sai đề nên mình ko giải được, bạn thông cảm nha
PT
1
CM
1 tháng 9 2019
Đặt m = x 2 .Điều kiện m ≥ 0
Ta có: 1/3. x 4 - 1/2. x 2 +1/6 =0⇔ 2 x 4 -3 x 2 +1=0 ⇔ 2 m 2 -3m + 1 =0
Phương trình 2 m 2 -3m + 1 =0 có hệ số a=2,b=-3,c=1 nên có dạng a +b+c =0
suy ra: m 1 = 1 , m 2 = 1/2
Ta có: x 2 = 1 ⇒ x = ± 1
x 2 = 1/2 ⇒ x = ± 2 /2
Vậy phương trình đã cho có 4 nghiệm :
x 1 =1 ; x 2 =-1 ; x 3 =( 2 )/2; x 4 = - 2 /2