A. 2
B. 3
C.4
D.1
giúp emm với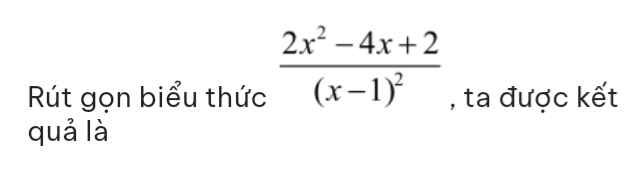 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PH
3
ND
2 tháng 5 2023
(a+1)+(a+2)+(a+3)=30
(a+a+a)+(1+2+3)=30
a+a+a+6=30
a+a+a=30-6
a+a+a=24
a=24:3
a=8
DH
21 tháng 2 2021
gọi đường thẳng qua M là Δ có vecto n là (a;b) đk a2+b2 ≠ 0
PTTQ của đg đi qua M là a(x-1)+b(y-2)=0 *
ta có CT tính góc giữa hai 2 đt
cos (Δ ;d ) = \(\dfrac{\left|3a-2b\right|}{\sqrt{a^2+b^2}.\sqrt{3^2+\left(-2\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(2\left|3a-2b\right|=\sqrt{26}\sqrt{a^2+b^2}\)
\(4\left(9a^{2^{ }}+4b-12ab\right)=26\sqrt{a^2+b^2}\)
\(10a^2-48ab-10b^2=0\)
(hd bấm máy tính bạn bấm pt bậc 2 các hệ số lần lượt là a = 10 ,b=-48,c=-10 ra kq là x= 5 và -1:5 ròi ghi a=5b và a=-1:5b nha )
\(\left[{}\begin{matrix}a=5b\\a=-\dfrac{1}{5}b\end{matrix}\right.\)
th1 vs a=5b
chọn b=1 =>a =5 thế vào * => pt đt qua M (ở đây bạn thích chọn b= số nào cx đc nha mình chọn 1 vì tốn giản thôi ở dưới cx tương tự )
th2 vs a=-\(\dfrac{1}{5}\)b
chọn b=-5 => a = 1 thế vào * => pt đt qua M
7 tháng 11 2021
\(a,=3\left(x^2-2\right)\\ b,=\left(x-1\right)^2-y^2=\left(x-y-1\right)\left(x+y-1\right)\\ c,=9x^2\left(x-y\right)-4\left(x-y\right)=\left(3x-2\right)\left(3x+2\right)\left(x-y\right)\\ d,=x\left(x^2-2x-8\right)=x\left(x^2+2x-4x-8\right)=x\left(x+2\right)\left(x-4\right)\)
1 tháng 3 2018
Hình vẽ minh họa nhé !
A B C 40 o
Xét \(\Delta ABC\) cân tại A có :
\(\widehat{B}=\widehat{C}=40^o\) (tính chất tam giác cân)
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (tổng 3 góc của 1 tam giác)
=> \(\widehat{A}+40^o+40^o=180^o\)
=> \(\widehat{A}=180^o-\left(40^o+40^o\right)\)
\(\Rightarrow\widehat{A}=100^o\)
TD
1 tháng 3 2018
Vì \(_{^{ }\dfrac{ }{ }\Delta}\)ABC cân tại A =) B=C = 40\(^0\)
A = \(\dfrac{180^0-B}{2}\)= 100\(^0\)
Vậy B= 40 \(^0\), A = 100\(^0\)
p/s : K bt vt góc
17 tháng 8 2023
1)
a) \(...=4^4-225=256-225=31\)
b) \(...=8.9.5+120=360-120=240\)
c) \(...=3^4-3^3=81-27=54\)
d) \(...=7^2-1=49-1=48\)
2) a) \(...=2^6=64\)
b) \(...=3^{15}:3^{10}=3^5=243\)
c) \(...=3^3-3^3=0\)
d) \(...=6^3+4^5=216+1024=1240\)
3 tháng 7 2019
Ta có \(a^4+ab^3=2a^3b^2\)
Do a>0
=> \(a^3+b^3=2a^2b^2\)
<=> \(\frac{a}{b^2}+\frac{b}{a^2}=2\)
Đặt \(\frac{a}{b^2}=x;\frac{b}{a^2}=y\)(x,y là số hữu tỉ)
=>\(\hept{\begin{cases}x+y=2\\x.y=\frac{1}{ab}\end{cases}}\)=> \(\hept{\begin{cases}x=2-y\\xy=\frac{1}{ab}\end{cases}}\)
=> \(\sqrt{1-\frac{1}{ab}}=\sqrt{1-y\left(2-y\right)}=\sqrt{y^2-2y+1}=|y-1|\)là số hữu tỉ
=> ĐPCM
Vậy \(\sqrt{1-\frac{1}{ab}}\)là số hữu tỉ
17 tháng 8 2023
bài này dễ mà bạn bạn chỉ cần đổi ra rồi tính bình thường là đc mà
HQ
Hà Quang Minh
Giáo viên
17 tháng 8 2023
Bài 1:
\(A=2^2\cdot3-4\\ =4\cdot3-4\\ =4\cdot\left(3-1\right)\\ =4\cdot2\\ =8\\ B=16-2^3\cdot2\\ =16-16\\ =0\\ C=4^2-4\cdot2\\ =4\cdot\left(4-2\right)\\ =4\cdot2\\ =8\\ D=3^3-3\cdot3^2\\ =3^3-3^3\\ =0\)
\(\dfrac{2x^2-4x+2}{\left(x-1\right)^2}=\dfrac{2\left(x^2-2x+1\right)}{\left(x-1\right)^2}=\dfrac{2.\left(x-1\right)^2}{\left(x-1\right)^2}=2\\ \RightarrowĐáp.án.A\)
2