Trong các số sau: 5895; 7950; 300; 57654; 6980; 8647; 6470; 8692; 20560; 8426; 8832
a) Tìm các số chia hết cho cả 2 và 5
b) Tìm các số chia hết cho cả 2 và 3
c) Tìm các số chia hết cho cả 2, 3 và 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy 1! + 2! = 3 \(⋮\) 3, còn từ 3! trở đi đương nhiên đều chia hết cho 3.
Do đó p2 + q2 + 5895 \(⋮\) 3. Mà 5895 \(⋮\) 3 nên p2 + q2 \(⋮\) 3 (1).
Lại có: p2 và q2 chia cho 3 dư 0 hoặc dư 1 do chúng đều là số chính phương (2).
Từ (1) và (2) \(\Rightarrow\) p2 \(⋮\) 3 và q2 \(⋮\) 3 \(\Rightarrow\) p \(⋮\) 3 và q \(⋮\) 3. Mà p và q là các snt nên p = q = 3 \(\Rightarrow\) 1! + 2! + 3! + ... + n! = 5913.
Vì n! < 5913 nên n < 8 \(\Rightarrow\) n \(\in\) {1; 2; 3; 4; 5; 6; 7}. Thử n với các số đó ta chỉ có n = 7 thỏa mãn.
Vậy n = 7.

Tớ làm đây r mà bạn:
Câu hỏi của Lev Ivanovich Yashin - Toán lớp 6 | Học trực tuyến

Rút gọn các phân số về phân số tối giản, sau đó so sánh để tìm ra phân số không bằng các phân số còn lại.
Ta rút gọn các phân số về dạng tối giản:
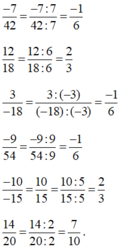
Do vậy ta có: 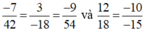
Phân số 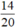 không bằng phân số nào trong các phân số còn lại.
không bằng phân số nào trong các phân số còn lại.
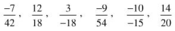
a) 7950 ; 300 ; 6980 ; 6470 ; 20560
b) 7950 ; 300 ; 57654 ; 8832
c) 7950 ; 300
a) 7950, 300, 6980, 6470, 20560
b) 7950, 300, 57654, 8832
c) 7950, 300