(z2 + 2z + 1/z2 + 2z +2) + (z2 + 2z + 2/ z2 + 2z +3) = 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
Cho z1; z2; z3; z4 là các nghiệm của phương trình: (z2 +1) (z2 - 2z + 2) = 0 . Tính 
A.5
B.4
C.-2
D.3
1
CM
4 tháng 6 2017
Chọn C.
PT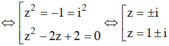 
S= i2014+ ( -i) 2014+ ( 1-i) 2014+ (1+ i) 2014
= ( i2) 1007+ [(-i)2]1007+ (-2i) 1007+ (2i) 1007= -1-1+( -2) 1007. i1007+ 21007. i1007= - 2
CM
10 tháng 6 2019
Đáp án A
PT ⇔ [ z = 1 + i z = 1 - u ⇒ z 1 = 1 + i z 2 = 1 - i ⇒ z 1 + z 2 = 2 z 1 - z 2 = 2 i ⇒ z 1 + z 2 = 2 z 1 - z 2 = 2 ⇒ P = 6
CM
25 tháng 9 2018
Đáp án D
Giả sử z = x + y i , x , y ∈ ℝ . Từ giả thiết ta có 2 x + y i − i = 2 + i x + y i
⇔ 2 x + 2 y − 1 i = 2 − y + x i ⇔ 4 x 2 + 2 y − 1 2 = y − 2 2 + x 2 ⇔ x 2 + y 2 = 1
Suy ra tập hợp các điểm A, B biểu diễn hai số phức z 1 , z 2 là đường tròn tâm O 0 ; 0 , bán kính R = 1 = O A = O B .
Giả sử z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i , a 1 , a 2 , b 1 , b 2 ∈ ℝ . Khi đó A a 1 ; b 1 , B a 2 ; b 2 .
Từ giả thiết z 1 − z 2 = 1 ta được:
a 1 − a 2 + b 1 − b 2 i = 1 ⇔ a 1 − a 2 2 + b 1 − b 2 2 = 1 ⇔ A B = 1
Từ đó O A = O B = A B ⇒ Δ O A B đều cạnh bằng 1.
Gọi M là trung điểm AB thì M a 1 + b 1 2 ; a 2 + b 2 2 và O M = A B 3 2 = 3 2 .
Khi đó
P = z 1 + z 2 = a 1 + a 2 + b 1 + b 2 i = a 1 + a 2 2 + b 1 + b 2 2
= 2 a 1 + a 2 2 2 + b 1 + b 2 2 2 = 2 O M = 2. 3 2 = 3
CM
2 tháng 11 2019
Chọn D.
Ta có: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 = 0
Hay ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) + z2 – 4z2 = 0
[(z2 + 3z + 6) + z]2 - ( 2z)2 = 0
[z2 + 4z + 6 ]2 - ( 2z)2 = 0
Suy ra: (z2 + 4z + 6 - 2z) (z2 + 4z + 6 + 2z) = 0
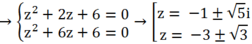
Vậy nghiệm của phương trình là: 
