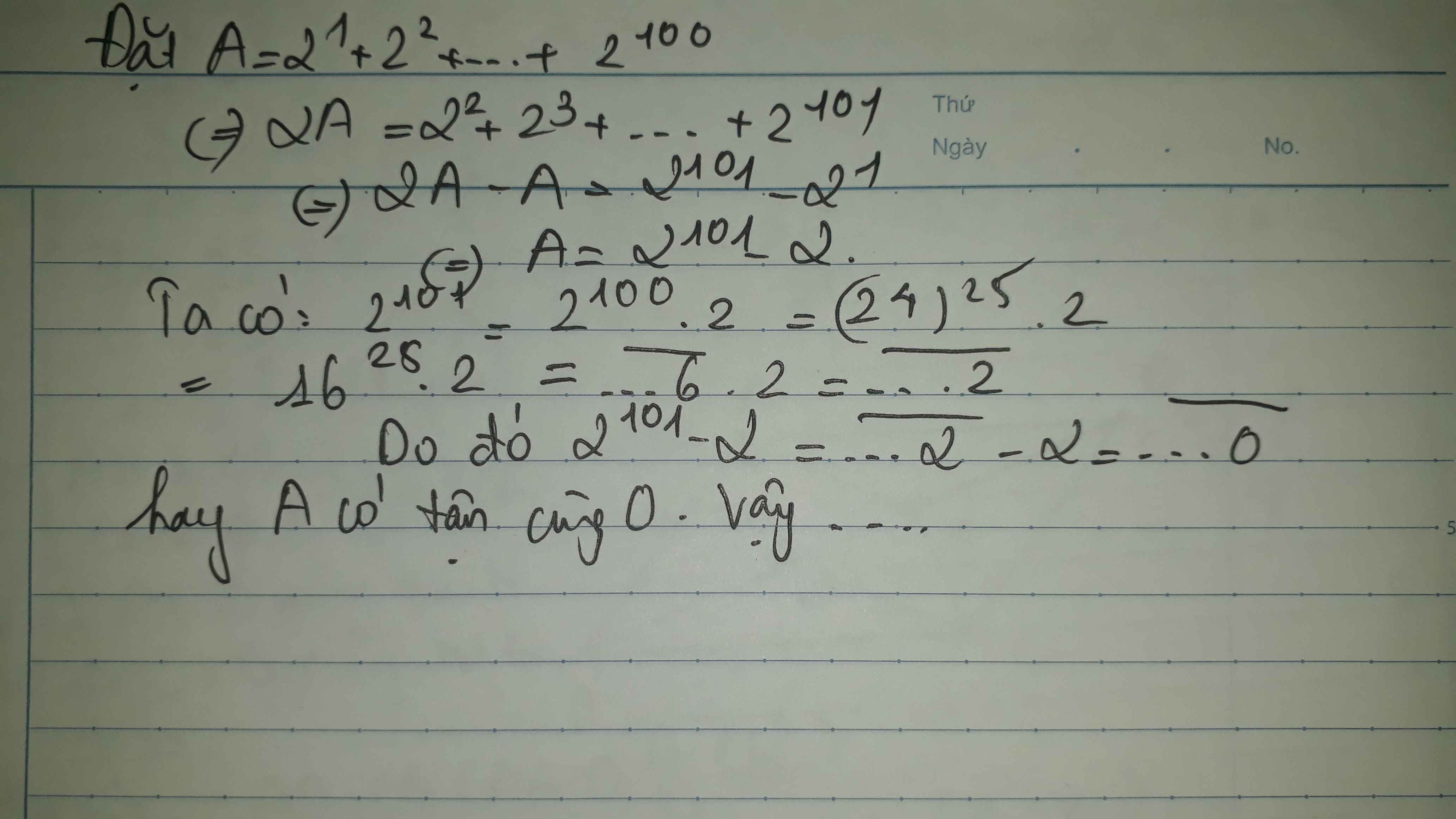tìm 2 c/s tận cùng của 2100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NG
2
5 tháng 9 2023
1) \(S=2.2.2..2\left(2023.số.2\right)\)
\(\Rightarrow S=2^{2023}=\left(2^{20}\right)^{101}.2^3=\overline{....6}.8=\overline{.....8}\)
2) \(S=3.13.23...2023\)
Từ \(3;13;23;...2023\) có \(\left[\left(2023-3\right):10+1\right]=203\left(số.hạng\right)\)
\(\) \(\Rightarrow S\) có số tận cùng là \(1.3^3=27\left(3^{203}=\left(3^{20}\right)^{10}.3^3\right)\)
\(\Rightarrow S=\overline{.....7}\)
3) \(S=4.4.4...4\left(2023.số.4\right)\)
\(\Rightarrow S=4^{2023}=\overline{.....4}\)
4) \(S=7.17.27.....2017\)
Từ \(7;17;27;...2017\) có \(\left[\left(2017-7\right):10+1\right]=202\left(số.hạng\right)\)
\(\Rightarrow S\) có tận cùng là \(1.7^2=49\left(7^{202}=7^{4.50}.7^2\right)\)
\(\Rightarrow S=\overline{.....9}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 9 2023
Bài 1:
S = 2 x 2 x 2 x 2 x 2 x...x 2 (2023 chữ số 2)
Nhóm 4 thừa số 2 vào một nhóm thì vì:
2023 : 4 = 505 dư 3
Vậy
S = (2x2x2x2) x...x (2 x 2 x 2 x 2) x 2 x 2 x 2 có 503 nhóm (2x2x2x2)
S = \(\overline{..6}\) x ...x \(\overline{..6}\) x 8
S = \(\overline{..6}\) x 8
S = \(\overline{..8}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 9 2023
Bài 2:
S = 3 x 13 x 23 x...x 2023
Xét dãy số: 3; 13; 23;..;2023
Dãy số trên là dãy số cách đều với khoảng cách là: 13 - 3 = 10
Số số hạng của dãy số trên là: (2023 - 3):10 + 1 = 203 (số hạng)
Vậy chữ số tận cùng của S bằng chữ số tận cùng của A.
Với A = 3 x 3 x 3 x...x 3 (203 thừa số 3)
Nhóm 4 thừa số 3 thành 1 nhóm, vì 203 : 4 = 50 (dư 3)
A = (3 x 3 x 3 x 3)x...x(3x3x3x3)x3x3x3 có 50 nhóm (3x3x3x3)
A = \(\overline{..1}\) x...x \(\overline{..1}\) x 27
A = \(\overline{..7}\)
22 tháng 8
Bài 6:
Với \(a=0\), ta có \(10^0+168=1+168=169=13^2\) , do đó ta tìm được cặp \(\left(a,b\right)=\left(0,13\right)\).
Với \(a\ge1\) thì \(10^{a}\) có chữ số tận cùng là 0, do đó \(10^{a}+168\) sẽ có chữ số tận cùng là 8, trong khi vế phải \(b^2\) lại là một số chính phương không thể có chữ số tận cùng là 8, mâu thuẫn. Vậy với \(a\ge1\) thì không có cặp \(\left(a,b\right)\) thỏa mãn điều kiện đã cho.
Vậy ta tìm được cặp số \(\left(a,b\right)\) duy nhất là \(\left(0,13\right)\).
W
1
LT
0
DN
1
TT
2