neu cach cm 1 tam giac la tam giac can
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
17 tháng 8 2023
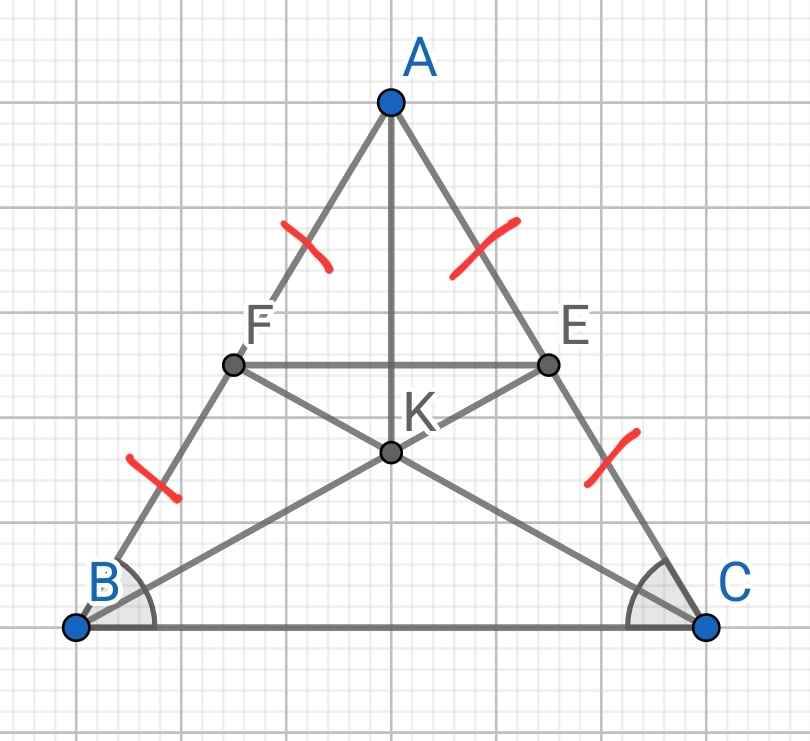1.
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB (1)
Do BE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AC
⇒ AE = CE = AC/2 (2)
Do CF là đường trung tuyến của ∆ABC (gt)
⇒ F là trung điểm của AB
⇒ AF = BF = AB/2 (3)
Từ (1), (2) và (3) ⇒ BF = CE
Do ∠ABC = ∠ACB (cmt)
⇒ ∠FBC = ∠ECB
Xét ∆BFC và ∆CEB có:
BF = CE (cmt)
∠FBC = ∠ECB (cmt)
BC chung
⇒ ∆BFC = ∆CEB (c-g-c)
⇒ CF = BE (hai cạnh tương ứng)
Hay BE = CF
b) Do ∆BFC = ∆CEB (cmt)
⇒ ∠BCF = ∠CBE (hai góc tương ứng)
⇒ ∠BCK = ∠CBK
∆BKC có:
∠BCK = ∠CBK (cmt)
⇒ ∆BKC cân tại K
c) Do ∆BKC cân tại K (cmt)
⇒ BK = CK
Do ∠ABC = ∠ACB (cmt)
⇒ ∠ABK = ∠ABC - ∠CBK = ∠ACB - ∠BCK = ∠ACK
⇒ ∠FBK = ∠ECK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
∠FBK = ∠CEK (cmt)
BF = CE (cmt)
⇒ ∆BFK = ∆CEK (c-g-c)
⇒ FK = EK (hai cạnh tương ứng)
d) Sửa đề: Chứng minh ∆BFK = ∆CEK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
BF = CE (cmt)
FK = EK (cmt)
⇒ ∆BFK = ∆CEK (c-c-c)
2.
a) Từ (1), (2) và (3) ⇒ AF = AE
∆AEF có:
AE = AF (cmt)
⇒ ∆AEF cân tại A
b) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (4)
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF = (180⁰ - ∠FAE) : 2
⇒ ∠AFE = ∠AEF = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠ABC = ∠AFE
Mà ∠ABC và ∠AFE là hai góc đồng vị
⇒ EF // BC
c) Xét ∆AFK và ∆AEK có:
AF = AE (cmt)
AK chung
FK = EK (cmt)
⇒ ∆AFK = ∆AEK (c-c-c)
DL
11 tháng 7 2017
Tam giác ABC có 50 cm nghĩa là sao bạn ? Cạnh nào của tam giác ABC ?
7 tháng 7 2022
a: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
DO đó; ΔABD cân tại A
b: Ta có: \(\widehat{MCB}=90^0-\widehat{CDM}\)
\(\widehat{ACB}=90^0-\widehat{ABC}=90^0-\widehat{ADH}=90^0-\widehat{CDM}\)
=>góc MCB=góc ACB
hay CB là phân giác của góc AMC
c: Xét ΔCAQ có
CH là đường phân giác
CH là đường cao
Do đó: ΔCAQ cân tại C