Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


để phương trình không là phương trình bậc nhất 1 ẩn thì m2 - m + 1=0
<=> (m2 - m + \(\frac{1}{4}\)) + \(\frac{3}{4}\)=0
<=> (m - \(\frac{1}{2}\))2 + \(\frac{3}{4}\)= 0 (1)
mà (m - \(\frac{1}{2}\))2 luôn luôn lớn hơn bằng 0 với mọi m
<=> (m - \(\frac{1}{2}\))2 +\(\frac{3}{4}\)>=\(\frac{3}{4}\)với mọi m (2)
từ (1) và (2) => không tồn tại m để phương trình đã cho không là phương trình bậc nhất 1 ẩn

dạ mình cám ơn ạ nma cho mình hỏi chút cái chỗ 2x1+x2=3 và x1+x2= gì v ạ

\(\hept{\begin{cases}2m^2x+3\left(m-1\right)y=3\\m\left(x+y\right)-2y=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2m^2x+3\left(m-1\right)y=3\\y\left(m-2\right)=2-mx\end{cases}}\)
Với m = 2 thì hệ trở thành
\(\hept{\begin{cases}8x+3y=3\\2-2x=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\y=\frac{-5}{3}\end{cases}}\)
Với \(m\ne2\)thì
\(\Leftrightarrow\hept{\begin{cases}2m^2x+3\left(m-1\right).\frac{2-mx}{\left(m-2\right)}=3\left(1\right)\\y=\frac{2-mx}{\left(m-2\right)}\left(2\right)\end{cases}}\)
Từ (1) ta có
\(\left(2m^3-7m^2+3m\right)x=-3m\)
Với \(\hept{\begin{cases}2m^3-7m^2+3m=0\\-3m=0\end{cases}}\Leftrightarrow m=0\)
Thì phương trình có vô số nghiệm (x,y) thõa y = - 1; x tùy ý
Với \(\hept{\begin{cases}2m^3-7m^2+3m=0\\-3m\ne0\end{cases}}\Leftrightarrow\orbr{\begin{cases}m=\frac{1}{2}\\m=3\end{cases}}\)
Thì hệ pt vô nghiệm
Với \(\hept{\begin{cases}2m^3-7m^2+3m\ne0\\-3m\ne0\end{cases}}\Leftrightarrow m\ne0;0,5;3\)
Thì hệ có nghiệm là
\(\hept{\begin{cases}x=\frac{3-3\left(m-1\right).\frac{2-mx}{\left(m-2\right)}}{2m^2}\\y=\frac{2-mx}{\left(m-2\right)}\end{cases}}\)
\(\hept{\begin{cases}2m^2x+3\left(m-1\right)y=3\\m\left(x+y\right)-2y=2\end{cases}}\)
Với m = 2 thì e giải nhé
Với m khác 2 thì
\(\Leftrightarrow\hept{\begin{cases}2m^2x+3\left(m-1\right).\frac{2-mx}{m-2}=3\left(1\right)\\y=\frac{2-mx}{m-2}\left(2\right)\end{cases}}\)
Xét (1) quy đồng rồi chuyển cái có x sang 1 vế phần còn lại sang 1 vế. Rồi biện luận nhé

\(a,\Delta=4\left(m-1\right)^2-4\left(-2m-3\right)=4m^2-8m+4+8m+12\\ \Delta=4m^2+16>0\left(đpcm\right)\\ b,\Delta=\left(2m-1\right)^2-4\left(2m-2\right)=4m^2-4m+1-8m+8\\ \Delta=4m^2-12m+9=\left(2m-3\right)^2\ge0\left(đpcm\right)\\ c,Sửa:x^2-2\left(m+1\right)x+2m-2=0\\ \Delta=4\left(m+1\right)^2-4\left(2m-2\right)=4m^2+8m+4-8m+8\\ \Delta=4m^2+12>0\left(đpcm\right)\\ d,\Delta=4\left(m+1\right)^2-4\cdot2m=4m^2+8m+4-8m\\ \Delta=4m^2+4>0\left(đpcm\right)\\ e,\Delta=4m^2-4\left(m+7\right)=4m^2-4m+7=\left(2m-1\right)^2+6>0\left(đpcm\right)\\ f,\Delta=4\left(m-1\right)^2-4\left(-3-m\right)=4m^2-8m+4+12+4m\\ \Delta=4m^2-4m+16=\left(2m-1\right)^2+15>0\left(đpcm\right)\)

b, pt \(\Leftrightarrow\)mx - 2=0
Nếu m=0 pt\(\Leftrightarrow\) -2=0 (vô lí)\(\Rightarrow\)m=2(loại)
Nếu m\(\ne\)0 pt có nghiệm x=\(\dfrac{2}{m}\)

A.(2x-5)=2x3-7x2+9x-10
\(\Rightarrow\)A = 2x3-7x2+9x-10 : (2x-5)
Bạn thực hiện chia đa thức cho đa thức được bao nhiêu đó là A

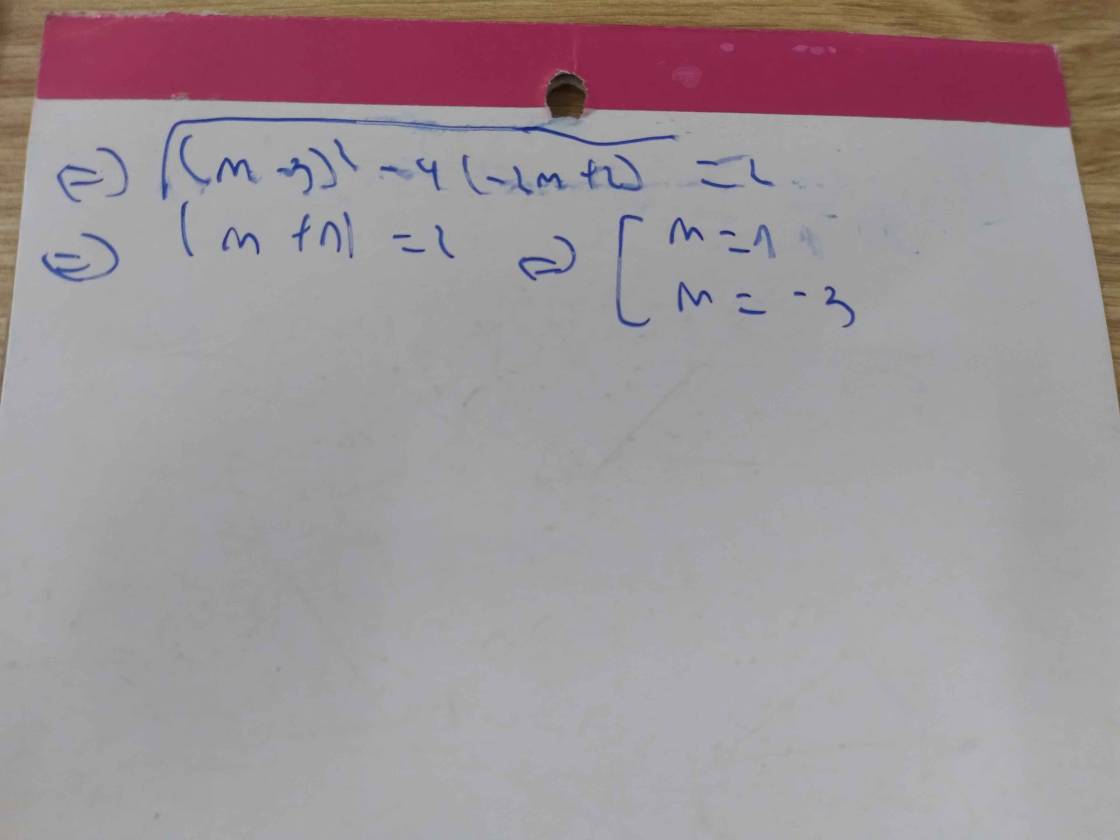
 Bạn tham khảo nhé
Bạn tham khảo nhé
\(\dfrac{2m+3}{m+2}-\dfrac{m}{m+2}=3\) (m \(\ne\) -2)
\(\Leftrightarrow\) \(\dfrac{m+3}{m+2}=3\)
\(\Leftrightarrow\) m + 3 = 3(m + 2)
\(\Leftrightarrow\) m + 3 = 3m + 6
\(\Leftrightarrow\) 2m = -3
\(\Leftrightarrow\) m = \(\dfrac{-3}{2}\) (TM)
Vậy ...
Chúc bn học tốt!