vẽ hộ mình cái hình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 9 2018
B A x x' y y' t t' 1 1 z
Chứng minh: At // Bt'
ta có: góc xAB = góc yBz ( đồng vị)
=> góc xAB/2 = góc yBz/2
mà góc A1 = góc xAB/2 ( tính chất tia phân giác)
góc B1 = góc yBz/2 ( tính chất tia phân giác)
=> góc A1 = góc B1 ( = góc xAB/2 = gocs yBz/2)
mà góc A1; góc B1 nằm ở vị trí đồng vị
=> At // Bt' ( định lí song song)
A
0
20 tháng 1 2024
Xét ΔDEF có DE<DF<EF
mà \(\widehat{F};\widehat{E};\widehat{D}\) lần lượt là góc đối diện của các cạnh DE,DF,EF
nên \(\widehat{F}< \widehat{E}< \widehat{D}\)
G
2
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
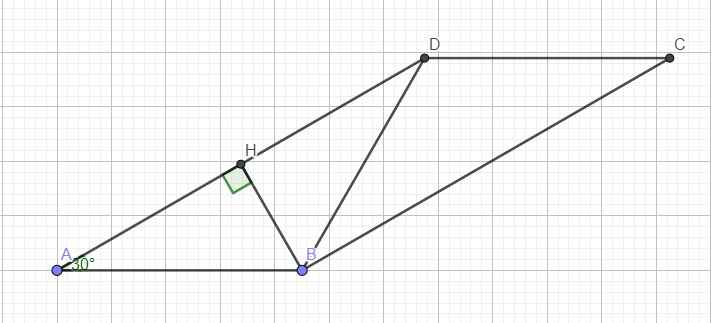
Kẻ đường cao BH ứng với AD
Do \(AB=AD\Rightarrow\Delta ABD\) cân tại B
\(\Rightarrow\) BH là đường cao đồng thời là trung tuyến
\(\Rightarrow AH=HD=\dfrac{1}{2}AD\)
Trong tam giác vuông ABH ta có:
\(sinA=\dfrac{BH}{AB}\Rightarrow BH=AB.sinA=18.sin30^0=9\left(cm\right)\)
\(cosA=\dfrac{AH}{AB}\Rightarrow AH=AB.cosA=18.cos30^0=9\sqrt{3}\left(cm\right)\)
\(\Rightarrow AD=2AH=18\sqrt{3}\left(cm\right)\)
\(S_{ABCD}=BH.AD=162\sqrt{3}\left(cm^2\right)\)
14 tháng 3 2023
a: OA<OB
=>A nằm giữa O và B
=>OA+AB=OB
=>AB=2cm
b: Vì OA<OC
nên A nằm giữa O và C
mà OA=1/2OC
nên A là trung điểm của OC