Cho tam giác ABC . 3 đường trung tuyến AD; BE;CF. Từ F kẻ dường thẳng song song với AD cắt ED kéo dài tại I.
A,CM: IC//BF
B,so sánh các cạnh của tam giác ICF với với trung tuyến tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
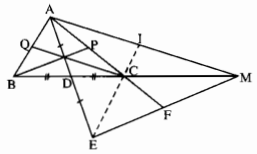
a) Do AD = DE nên MD là một đường trung tuyến của tam giác AEM. Hơn nữa do
CD=12CB=12CMCD=12CB=12CM
Nên C là trọng tâm của tam giá AEM.
b) Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I. Tam giác AEM có các đường trung tuyến là AF, EI, MD. Ta có ∆ADB = ∆EDG (c.g.c) nên AB = EC
Vậy: AC=23AF;BC=CM=23MD;AB=EC=23EIAC=23AF;BC=CM=23MD;AB=EC=23EI
c) Trước tiên, theo giả thiết, ta có AD = DE nên AD=12AEAD=12AE
Gọi BP, CQ là các trung tuyến của ∆ABC.
∆BCP = ∆MCF => BP=FM=12EMBP=FM=12EM. Ta sẽ chứng minh CQ=12AMCQ=12AM
Ta có:
ΔABD=ΔECD⇒ˆBAD=ˆCED⇒AB//EC⇒ˆQAC=ˆICAΔABD=ΔECD⇒BAD^=CED^⇒AB//EC⇒QAC^=ICA^
Hai tam giác ACQ và CAI có cạnh AC chung, ˆQAC=ˆICAQAC^=ICA^;
AQ=12AB=12EC=ICAQ=12AB=12EC=IC nên chúng bằng nhau.
Vậy CQ=AI=12AMCQ=AI=12AM.
Tóm lại: AD=12AE,BP=12EM,CQ=12AM

Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I. Tam giác AEM có các đường trung tuyến là AF, EI, MD. Ta có ΔADB = ΔEDC (c.g.c) nên AB = EC
Vậy: AC = 2/3 AF; BC = CM = 2/3 MD; AB = EC = 2/3 EI

A B C D E G N M P F
Gọi AM, BN, CP là các đường trung tuyến của ∆ABC cắt nhau tại G.
AG = GD (gt)
AG = 2GM (suy ra từ tính chất đường trung tuyến)
Nên GD = 2GM
GD = GM + MD
=> GM = MD
Xét ∆BMD và ∆CMG:
BM = CM (gt)
\(\widehat{BND}=\widehat{CMG}\left(\text{đối đỉnh}\right)\)
MD = GM (chứng minh trên)
Do đó: ∆BMD = ∆CMG (c.g.c)
=> BD = CG
\(CG=\frac{2}{3}CP\left(\text{tính chất đường trung tuyến}\right)\)
\(\Rightarrow BD=\frac{2}{3}CP\) (1)
\(BG=\frac{2}{3}BN\left(\text{tính chất đường trung tuyến}\right)\) (2)
\(AG=\frac{2}{3}AM\left(\text{tính chất đường trung tuyến}\right)\)
\(\Rightarrow GD=\frac{2}{3}AM\) (3)
Từ (1), (2) và (3) suy ra các cạnh của \(\Delta BGD=\frac{2}{3}\) các đường trung tuyến của \(\Delta ABC\)
GM = MD (chứng minh trên)
Nên BM = MD là đường trung tuyến của ∆BGD
\(BM=\frac{1}{2}BC\) (4)
Kẻ đường trung tuyến GE và DF của ∆BGD
\(\Rightarrow FG=\frac{1}{2}BG\)
\(GN=\frac{1}{2}BG\left(\text{tính chất đường trung tuyến}\right)\)
Nên FN = GN
Xét ∆DFG và ∆ANG:
AG = GD (gt)
\(\widehat{DGF}=\widehat{AGN}\left(\text{đối đỉnh}\right)\)
GF = GN (chứng minh trên)
Do đó ∆DFG = ∆ANG (c.g.c)
=> DF = AN
\(AN=\frac{1}{2}AC\left(gt\right)\)
\(\Rightarrow DF=\frac{1}{2}AC\) (5)
BD = CG (chứng minh trên)
\(ED=\frac{1}{2}BD\left(\text{vì E là trung điểm BD}\right)\)
\(GP=\frac{1}{2}CG\left(\text{tính chất đường trung tuyến}\right)\)
=> ED = GP
∆BDM = ∆CGM (chứng minh trên)
\(\Rightarrow\widehat{BDM}=\widehat{CGM}\text{ hay }\widehat{CGM}\)
\(\widehat{CGM}=\widehat{PGA}\left(\text{đối đỉnh}\right)\)
\(\Rightarrow\widehat{EDG}=\widehat{PGA}\)
AG = GD (gt)
=> ∆PGA = ∆EDG (c.g.c)
=> GE = AP
\(\Rightarrow GE=\frac{1}{2}AB\)(6)
Từ (4),(5) và (6) suy ra các đường trung tuyến của ∆BGD bằng một nửa cạnh của ∆ABC.