cho tam giác ABC vuông tại A, AB = 15cm và AC = 20cm . Gọi M là trung điểm của BC. Tính AM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2016
áp dụng định lí py ta go vào tam giác vuông abc vuông tại a . ta có
bc2 = ab2 + ac2
\(\Rightarrow\)bc2 = 152 + 202
\(\Rightarrow\)bc2 = 225 + 400
\(\Rightarrow\)bc2 = 625 = 252
\(\Rightarrow\)bc = 25
vi bm = mc \(\Rightarrow\)am là đường trung tuyến của bc(1)
mà tam giác abc vuông tại a (2)
tu 1 va 2 \(\Rightarrow\)am = 1/2 bc = 1/2 25 = 12,5 ( cm )
23 tháng 5 2021
Sao ý A nhiều ng bảo ko làm đc nhỉ???
Ta chỉ cần dùng tính chất bắc cầu là ra mà
6 tháng 3 2022
a:\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
2 tháng 11 2021
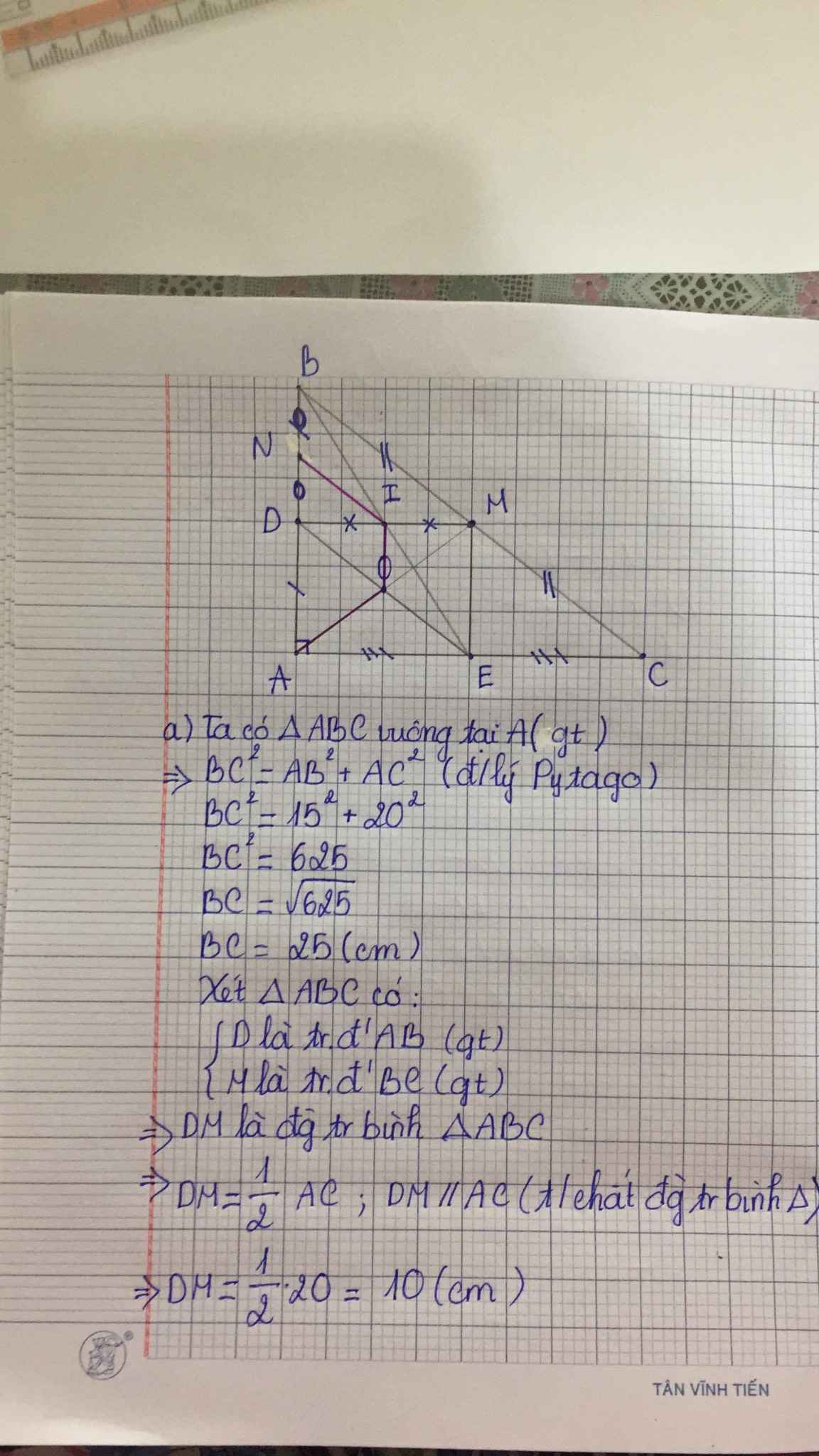
a: Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
hay BC=25(cm)
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình của ΔABC
Suy ra: \(DM=\dfrac{AC}{2}=10\left(cm\right)\)
6 tháng 5 2016
Chứng minh câu a)
Ta có: AH vuông góc với BC ( giả thiết)
=> góc H = 1v
Xét tam giác AHC và tam giác BHA có:
góc AHC=AHB=90 độ
góc B=góc C=45 độ
=>2 tam giác đồng dạng
Câu b)
*BC=?
Ta có tam giác ABC vuông tại A( theo giả thiết0
Theo định lí pi ta go, ta có :
BC^2=AC^2+AB^2=400+225=625
=>BC=25
*AH=?
S tam giác ABC=1/2.AB.AC hoặc 1/2BC.AH
=>AB.AC=BC.AH =>AB/BC=AH/AC
=>AH=15.20/25=12
Câu c)mk ko piet giai nha sorry nha
8 tháng 2 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC^2=15^2+20^2=625\)
hay BC=25(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot25=15\cdot20\)
\(\Leftrightarrow AH\cdot25=300\)
hay AH=12(cm)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=AC^2-AH^2=20^2-12^2=256\)
hay HC=16(cm)
Vậy: BC=20cm; AH=12cm; HC=16cm
8 tháng 4 2023
a: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc MAC+góc AED=90 độ
=>góc MAC+góc AHD=90 độ
=>góc MAC+góc B=90 độ
=>góc MAC=góc MCA và góc MAB=góc MBA
=>MA=MB=MC
=>M là trung điểm của BC
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=20^2/25=16(cm)
AD=12^2/15=144/15=9,6cm
AE=12^2/20=7,2cm
\(S_{ADE}=\dfrac{1}{2}\cdot7.2\cdot9.6=34.56\left(cm^2\right)\)
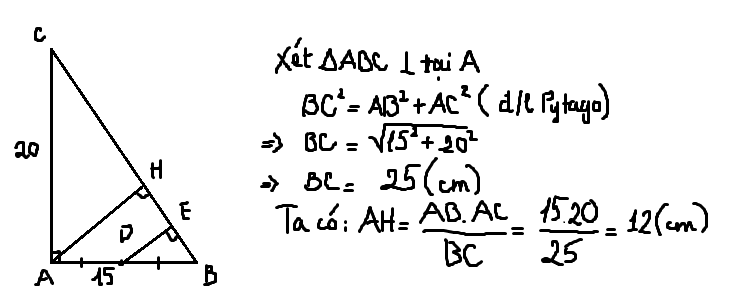
AM=12,5cm
áp dụng định lí pytago vào tam giác vuông abc vuông tại a. ta có:
bc2= ab2+ac2
\(=>\) bc2=152+202
\(=>\) bc2=225+400
\(=>\) bc2=625=252
\(=>\)bc=25
vì bm=mc \(=>\)am là đường trung tuyến của bc(1)
mà tam giác abc vuông tại a(2)
tu 1 và 2\(=>\)am=1/2 bc=1/2 25 = 12,5(cm)