Với x>0 thì giá trị nhỏ nhất của biểu thức M=9x2+3x+1/x là : ...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
I
2 tháng 3 2020
\(M=\)như trên
\(=>M=4x^2-4x+1+x+\frac{1}{4x}+2010\)
\(=>M=\left(4x^2-4x+1\right)+\left(x+\frac{1}{4x}\right)+2010\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\)
Áp dụng BĐT Cô- si cho 2 số không âm, ta có:
\(x+\frac{1}{4x}\ge2\sqrt{x.\frac{1}{4x}}=2\sqrt{\frac{1}{4}}=1\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\ge0+1+2010=2011\\ \)
=>minM=2011 khi x=\(\frac{1}{2}\)
CM
10 tháng 3 2019
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
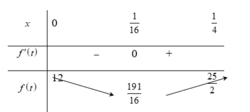
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
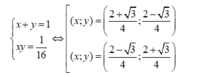
Chọn A.
12 tháng 2 2023
\(\text{Δ}=\left(2m-2\right)^2-4\left(m-5\right)\)
=4m^2-8m+4-4m+20
=4m^2-12m+24
=4m^2-12m+9+15
=(2m-3)^2+15>0
=>PT luôn có hai nghiệm
A=(x1+x2)^2-2x1x2
=(2m-2)^2-2(m-5)
=4m^2-8m+4-2m+10
=4m^2-10m+14
=4(m^2-5/2m+7/2)
=4(m^2-2*m*5/4+25/16+31/16)
=4(m-5/4)^2+31/4>=31/4
Dấu = xảy ra khi m=5/4
10 tháng 2 2019
P/s: ko chắc
\(P=\frac{x^2-x+1}{x^2+x+1}\)
\(P=\frac{x^2}{x^2+x+1}-\frac{x}{x^2+x+1}+\frac{1}{x^2+x+1}\)
\(P=x^2\cdot\frac{1}{x^2+x+1}-x\cdot\frac{1}{x^2+x+1}+\frac{1}{x^2+x+1}\)
\(P=\frac{1}{x^2+x+1}\left(x^2-x+1\right)\)
\(P=\frac{1}{x^2+x+1}\left[x^2-2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}\right]\)
\(P=\frac{1}{x^2+x+1}\left[\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\right]\)
\(P=\frac{1}{x^2+x+1}\cdot\left(x-\frac{1}{2}\right)^2+\frac{1}{x^2+x+1}\cdot\frac{3}{4}\)
Vì \(\frac{1}{x^2+x+1}\cdot\left(x-\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow P\ge\frac{1}{x^2+x+1}\cdot\frac{3}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{1}{x^2+x+1}\cdot\left(x-\frac{1}{2}\right)^2\Leftrightarrow x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}\)
Vậy...
10 tháng 2 2019
dễ hơn nè
Ta thấy x2 + x + 1 > 0
Ta có : 2 ( x - 1 )2 \(\ge\)0 \(\Rightarrow\)2x2 - 4x + 2 \(\ge\)0 \(\Rightarrow\)3 ( x2 - x + 1 ) \(\ge\)x2 + x + 1
\(\Rightarrow\frac{x^2-x+1}{x^2+x+1}\ge\frac{1}{3}\) . Dấu " = " xảy ra \(\Leftrightarrow\)x = 1
9x^2 +3x+1 tất cả chia cho x hay mỗi 1/x vậy bạn??
nếu là (9x^2+3x+1)/x thì mình giải nhá
chia cho x =) biểu thức trên sẽ bằng 9x+3+1/x
Áp dụng bất đẳng thức cosi của 9x và 1/x ta có : 9x+1/x lớn hơn hoặc bằng 2 căn bậc 2 của 9x nhân 1/x =) lớn hơn hoặc bằng 6
=) Min M = 3+ 6 =9 tại x= 1/3 và x= -1/3 nha bạn