Giúp em với ạ
Em cảm ơn 🥺🥺🥺
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
25 tháng 12 2021
\(Cau.23:\\ N=\left(A_1+T_1+G_1+X_1\right).2=\left(100+200=300+400\right).2=2000\left(Nu\right)\\ L=\dfrac{N}{2}.3,4=\dfrac{2000}{2}.3,4=3400\left(A^o\right)\\ Chon.C\)
N
29 tháng 10 2021
Bạn tự vẽ sơ đồ mạch điện và tự làm tóm tắt nhé!
Bài 1:
b. \(U=IR=I\left(R1+R2\right)=0,4\left(15+2\right)=6,8\left(V\right)\)
c. \(I=I1=I2=\dfrac{U'}{R}=\dfrac{60}{15+2}=\dfrac{60}{17}\simeq3,5\left(A\right)\left(R1ntR2\right)\)
Bài 2:
\(5400kJ=1500\left(Wh\right)\)
a. \(A=Pt\Rightarrow P=\dfrac{A}{t}=\dfrac{1500}{1}=1500\left(W\right)\)
b. \(P=UI\Rightarrow I=\dfrac{P}{U}=\dfrac{1500}{220}=\dfrac{75}{11}\simeq6,82\left(A\right)\)
N
29 tháng 10 2021
Bài 3:
a. \(R=p\dfrac{l}{S}=1,1.10^{-6}\dfrac{3}{0,05.10^{-6}}=66\left(\Omega\right)\)
b. \(P=UI=U\left(\dfrac{U}{R}\right)=220.\left(\dfrac{220}{66}\right)=733,33\left(W\right)\)
c. \(A=Pt=733,33.\left(\dfrac{30}{60}\right)=366,665\left(Wh\right)=0,366665\left(kWh\right)=1319994\left(J\right)\)
Bài 4:
a. \(S=\pi\dfrac{d^2}{4}=\pi\dfrac{1^2}{4}=0,785\left(mm^2\right)\)
\(\Rightarrow R=p\dfrac{l}{S}=5,5.10^{-8}\dfrac{10}{0,785.10^{-6}}=\dfrac{110}{157}\simeq0,7\left(\Omega\right)\)
b. \(A=Pt=UIt=U\left(\dfrac{U}{R}\right)t=70\left(\dfrac{70}{0,7}\right).\dfrac{1}{3}=2333,33\left(Wh\right)=2,33333\left(kWh\right)\simeq8400000\left(J\right)\)
31 tháng 10 2021
Câu 6:
\(U=I.R=10.1,5=15\left(V\right)\)
Câu 7:
\(P=U.I\Rightarrow U=\dfrac{P}{I}=\dfrac{10}{0,5}=20\left(V\right)\)
Câu 8:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{10.30}{10+30}=7,5\left(\Omega\right)\)
29 tháng 3 2021
- Về nội dung:
+ Liên kết chủ đề
+ Liên kết lôgic
- Về hình thức:+ Phép lặp
+ Phép đồng nghĩa, trái nghĩa, liên tưởng
+ Phép nối
+ Phép thế
- Phép liên kết sử dụng trong đoạn: phép thế (Ông - Họa sĩ)
AT
3 tháng 7 2021
2) \(\dfrac{\left(1+\sqrt{a}\right)^2-\left(2-\sqrt{a}\right)^2}{1-2\sqrt{a}}:\dfrac{\sqrt{a}}{3}\left(a>0,a\ne\dfrac{1}{4}\right)\)
\(=\dfrac{\left(1+\sqrt{a}-2+\sqrt{a}\right)\left(1+\sqrt{a}+2-\sqrt{a}\right)}{1-2\sqrt{a}}.\dfrac{3}{\sqrt{a}}\)
\(=\dfrac{3.\left(2\sqrt{a}-1\right)}{1-2\sqrt{a}}.\dfrac{3}{\sqrt{a}}=-\dfrac{9}{\sqrt{a}}\)
5) \(\left(5-\dfrac{a+3\sqrt{a}}{\sqrt{a}+3}\right)\left(2-\dfrac{3a+\sqrt{a}}{3\sqrt{a}+1}\right)\left(a\ge0\right)\)
\(=\left(5-\dfrac{\sqrt{a}\left(\sqrt{a}+3\right)}{\sqrt{a}+3}\right)\left(2-\dfrac{\sqrt{a}\left(3\sqrt{a}+1\right)}{3\sqrt{a}+1}\right)\)
\(=\left(5-\sqrt{a}\right)\left(2-\sqrt{a}\right)=10-7\sqrt{a}+a\)
6) \(\left(2-\dfrac{a-3\sqrt{a}}{\sqrt{a}-3}\right)\left(2-\dfrac{5\sqrt{a}-\sqrt{ab}}{\sqrt{b}-5}\right)\left(a,b\ge0,a\ne9,b\ne25\right)\)
\(=\left(2-\dfrac{\sqrt{a}\left(\sqrt{a}-3\right)}{\sqrt{a}-3}\right)\left(2+\dfrac{\sqrt{a}\left(\sqrt{b}-5\right)}{\sqrt{b}-5}\right)\)
\(=\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)=4-a\)
3 tháng 7 2021
3) Ta có: \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\)
\(=\sqrt{a}+2-\sqrt{a}-2\)
=0
31 tháng 10 2021
Câu 3:
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
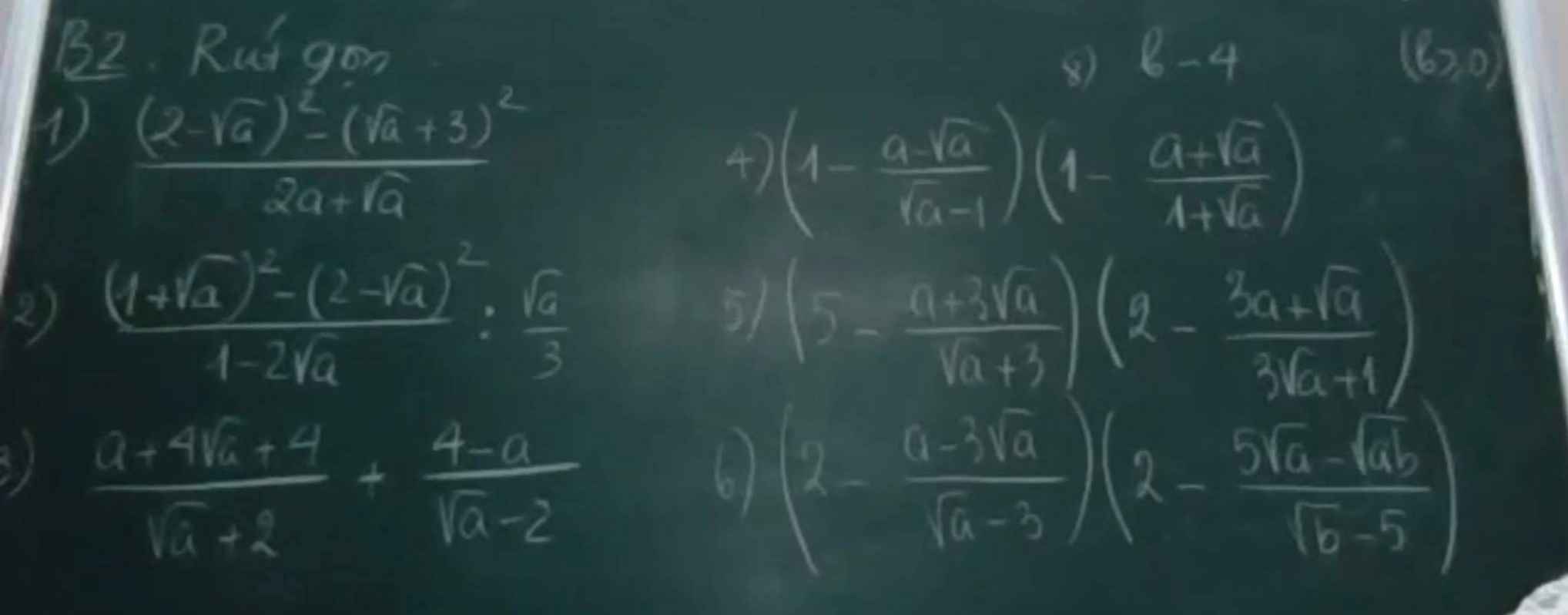
Câu 20: C
Câu 21: B