Cho A = x-1/2
Tìm x để A > 0; A < 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2023
P>1/3
=>P-1/3>0
=>\(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-\dfrac{1}{3}>0\)
=>\(\dfrac{3\sqrt{x}-3-\sqrt{x}-2}{3\left(\sqrt{x}+2\right)}>0\)
=>2 căn x-5>0
=>x>25/4
31 tháng 8 2021
a: Ta có: \(\sqrt{2x-1}=4\)
\(\Leftrightarrow2x-1=16\)
\(\Leftrightarrow2x=17\)
hay \(x=\dfrac{17}{2}\)
b: Ta có: \(\sqrt{4x+4}-\sqrt{9x+9}=-6\)
\(\Leftrightarrow-\sqrt{x+1}=-6\)
\(\Leftrightarrow x+1=36\)
hay x=35
30 tháng 7 2021
b) Thay x=2 vào pt, ta được:
\(4\left(m^2-1\right)-4m+m^2+m+4=0\)
\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)
\(\Leftrightarrow5m^2-3m=0\)
\(\Leftrightarrow m\left(5m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=\dfrac{2m}{m^2-1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)
19 tháng 12 2021
Để A là số nguyên thì \(2x-1\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{1;0;3;-2\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
Từ điều kiện đề bài \(\Rightarrow\left\{{}\begin{matrix}a+b+c=8\\-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=9\end{matrix}\right.\Rightarrow f\left(x\right)=-x^2+4x+5\)
a. Không tồn tại m để \(3\left|f\left(x\right)\right|+m-5=0\) có 3 nghiệm phân biệt (nếu pt đã cho có 3 nghiệm thì 1 nghiệm trong đó luôn là nghiệm kép). Có 3 nghiệm thì được (khi đó \(\dfrac{5-m}{3}=9\Rightarrow m\))
b. \(2f\left(\left|x\right|\right)-7+5m=0\Leftrightarrow f\left(\left|x\right|\right)=\dfrac{-5m+7}{2}\) (1)
Đồ thì hàm \(y=f\left(\left|x\right|\right)\) (tạo ra bằng cách bỏ phần bên trái trục Oy và lấy đối xứng phần bên phải của đồ thị \(y=f\left(x\right)\) qua):
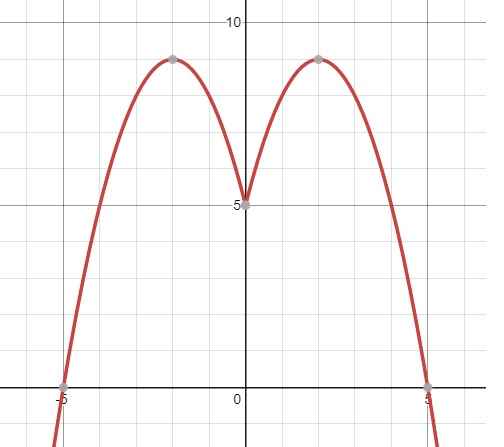
Từ đồ thị ta thấy (1) có 4 nghiệm pb khi:
\(5< \dfrac{-5m+7}{2}< 9\) \(\Rightarrow-\dfrac{11}{5}< m< -\dfrac{3}{5}\)
L
1
17 tháng 7 2021
\(\)áp dụng BĐT AM-GM(BÀi này ko có Max chỉ có Min)
\(=>\dfrac{1}{x}+\dfrac{1}{y}\ge2\sqrt{\dfrac{1}{xy}}=\dfrac{2}{\sqrt{xy}}\)
\(=>\dfrac{1}{2}\ge\dfrac{2}{\sqrt{xy}}=>\sqrt{xy}\ge4\)
\(=>S=\sqrt{x}+\sqrt{y}\ge2\sqrt{4}=4\)
dấu"=" xảy ra<=>x=y=4
LN
0
20 tháng 6 2018
a, Ta có :
\(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)
\(\Rightarrow\frac{(a+b)}{ab}\ge\frac{4}{(a+b)}\)
\(\Rightarrow(a+b)^2\ge4ab\)
\(\Rightarrow(a-b)^2\ge0(đpcm)\)
Mình để cho dấu lớn bằng để dễ hiểu nha bạn
c,Ta có : \(x^2-4x+5=(x^2-4x+4)+1=(x-2)^2+1\ge1\)
Dấu " = "xảy ra khi : \((x-2)^2=0\Rightarrow x=x-2=0\Rightarrow x=2\)
Rồi bạn tự suy ra.Mk chắc đúng không nữa nên bạn thông cảm
Còn câu b và d bạn tự làm nhé
Chúc bạn học tốt
20 tháng 6 2018
\(a,\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)
\(\Leftrightarrow\frac{a+b}{ab}-\frac{4}{a+b}\ge0\)
\(\Leftrightarrow\frac{a^2+2ab+b^2-4ab}{ab\left(a+b\right)}\ge0\)
\(\Leftrightarrow\frac{a^2-2ab+b^2}{ab\left(a+b\right)}\ge0\Leftrightarrow\frac{\left(a-b\right)^2}{ab\left(a+b\right)}\ge0\)(luôn đúng vì a>0,b>0)
dấu ''='' xảy ra khi và chỉ khi a=b
\(b,x+\frac{1}{x}\ge2\)
\(\Leftrightarrow x-2+\frac{1}{x}\ge0\)
\(\Leftrightarrow\frac{x^2-2x+1}{x}\ge0\Leftrightarrow\frac{\left(x-1\right)^2}{x}\ge0\)(luôn đúng)
dấu''='' xảy ra khi và chỉ khi x=1
áp dụng\(x+\frac{1}{x}\ge2\)(c/m trên) =>GTNN là 2
dấu ''='' xay ra khi và chỉ khi x=1
\(c,\Leftrightarrow\left(x-2\right)^2+1\ge1\)
=> GTNN là 1 tại x=2
\(d,\frac{-\left(x^2+4x+4+6\right)}{x^2+2018}=\frac{-\left(x+2\right)-6}{x^2+2018}< 0\)
vì -(x+2 )-6 <-6
VM
0
Answer:
Để \(A>0\)
\(\Rightarrow\frac{x-1}{2}>0\)
\(\Rightarrow x-1>0\)
\(\Rightarrow x>1\)
Vậy \(x>1\Leftrightarrow A>0\)
Để \(A< 0\)
\(\Rightarrow\frac{x-1}{2}< 0\)
\(\Rightarrow x-1< 0\)
\(\Rightarrow x< 1\)
Vậy \(x< 1\Leftrightarrow A< 0\)