Cho 7x=4y và y-x=24, giá trị của x là ...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
2
HP
25 tháng 11 2021
+ 7x = 4y
\(\Leftrightarrow y=\dfrac{7x}{4}\)
+ y - x = 24
\(\Leftrightarrow y=24+x\)
\(\Rightarrow24+x=\dfrac{7x}{4}\)
\(\Leftrightarrow x=32\)
19 tháng 3 2021
Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)
NA
2
26 tháng 7 2015
theo t/c đề bài ta có: x/4=y/7 và y-x=24
theo t/c dãy tỉ số bằng nhau ta có: x/4=y/7=y-x/7-4=6
=)x/4=6=)x=6.4=24
=)y/7=6=)y=6.7=42
vậy x=24 và y=42
chú ý là dấu chấm là dấu nhân
26 tháng 7 2015
\(7x=4y\) va y-x=24
\(7x=4y\Rightarrow\frac{x}{4}=\frac{y}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{7}=\frac{y-x}{7-4}=\frac{24}{3}=8\)
Suy ra : \(\frac{x}{4}=8\Rightarrow x=8.4=32\)
\(\frac{y}{7}=8\Rightarrow y=8.7=56\)
9 tháng 10 2017
Theo bài ra ta có :
\(7x=4y\Rightarrow\frac{x}{4}=\frac{y}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{x}{4}=\frac{y}{7}=\frac{y-x}{7-4}=\frac{24}{3}=8\)
\(\frac{x}{4}=8\Rightarrow x=32\)
\(\frac{y}{7}=8\Rightarrow y=56\)
Vậy x = 32 ; y = 56
9 tháng 10 2017
Ta có:
\(7x=4y\)và y-x=24
=>\(\frac{x}{4}=\frac{y}{7}\)và y-x=24
=>\(\frac{y}{7}=\frac{x}{4}\)và y-x=24
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{y}{7}=\frac{x}{4}=\frac{y-x}{7-4}=\frac{24}{3}=8\)
\(=>\hept{\begin{cases}\frac{y}{7}=8=>y=8.7=56\\\frac{x}{4}=8=>x=8.4=32\end{cases}}\)
Vậy \(\hept{\begin{cases}y=56\\x=32\end{cases}}\)
19 tháng 7 2023
\(1)A=2x\left(x-y\right)-y\left(y-2x\right)\)
\(=2x^2-2xy-y^2+2xy\)
\(=2x^2-y^2=2.\left(-\dfrac{2}{3}\right)^2-\left(-\dfrac{1}{3}\right)^2\)
\(=\dfrac{8}{9}-\dfrac{1}{9}=\dfrac{7}{9}\)
\(2)B=5x\left(x-4y\right)-4y\left(y-5x\right)\)
\(=5x^2-20xy-4y^2+20xy\)
\(=5x^2-4y^2=5.\left(-\dfrac{1}{5}\right)^2-4.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{5}-1=-\dfrac{4}{5}\)
\(3)C=\text{x.(x^2-y^2)-x^2(x+y)+y(x^2-x)}\)
\(=x^3-xy^2-x^3-x^2y+x^2y-xy\)
\(=-xy\left(x+1\right)\)
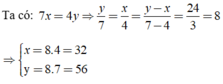
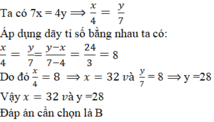
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{y-x}{7-4}=\dfrac{24}{3}=8\)
Do đó: x=32