Tìm các số nguyên x;y thoả mãn
a)x.(y+1)=-7
b)2.xy+x+y=7
Giúp mình câu này với(Lưu ý:Giải chi tiết)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để t = \(\frac{3x-8}{x-5}\)nguyên
=> 3x - 8 chia hết cho x - 5
=> 3x - 15 + 7 chia hết cho x - 5
=> 3(x - 5) + 7 chia hết cho x - 5
Có 3(x - 5) chia hết cho x - 5
=> 7 chia hết cho x - 5
=> x - 5 thuộc Ư(7)
=> x - 5 thuộc {1; -1; 7; -7}
=> x thuộc {6; 4; 12; -2}
Để T nguyên thì 3x - 8 chia hết cho x - 5
<=> 3x - 15 + 7 chia hết cho x - 5
=> 3(x - 5) + 7 chia hết cho x - 5
=> 7 chia hết cho x - 5
=> x - 5 thuộc Ư(7)={-1;1;-7;7}
Ta có:
| x - 5 | -1 | 1 | -7 | 7 |
| x | 4 | 6 | -2 | 12 |

6 là bội của n+1
=> 6 chia hết cho n+1
=> n+1 thuộc Ư(6)={-1,-2,-3,-6,1,2,3,6}
Ta có bảng :
| n+1 | -1 | -2 | -3 | -6 | 1 | 2 | 3 | 6 |
| n | -2 | -3 | -4 | -7 | 0 | 1 | 2 | 5 |
Vậy n={-7,-4,-3,-2,0,1,2,5}

Vì 12 chia hết cho x và 15 chia hết cho x
=> x thuộc ƯC(12,15)
Ta có: 12 = 22 . 3
15 = 3. 5
=> ƯCLN(12,15) = 3
=> ƯC(12,15) = {-3:-1:1:3}
12⋮x và 15⋮x => x ϵ ƯC(12,15)
12 = 22.3
15 = 3.5
=> ƯCLN(12,15) = 3
=> ƯC(12,15) = Ư(3) = {-3;-1;1;3}

Ta có x + 4 = (x + 1) + 3
nên (x + 4) ⋮ (x + 1) khi 3 ⋮ (x + 1), tức là x + 1 là ước của 3.
Vì Ư(3) = {-1; 1; -3; 3} ta có bảng sau:

Đáp số x = -4; -2; 0; 2.

Ta có các trường hợp:
+TH1: \(\left\{{}\begin{matrix}x+2>0\\x-1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x>1\end{matrix}\right.\)\(\Leftrightarrow x>1\)
+TH2: \(\left\{{}\begin{matrix}x+2< 0\\x-1< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< -2\\x< 1\end{matrix}\right.\)\(\Leftrightarrow x< -2\)
Vậy.....
(x+2) (x-1)>0 thì nó có cả đống bạn ạ VD:
(10+2)x(11-1)= 120 > 0

Ta có các trường hợp sau:
+TH1: \(\left\{{}\begin{matrix}x+3>0\\x-2< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x>-3\\x< 2\end{matrix}\right.\)\(\Leftrightarrow-3< x< 2\)
+TH2: \(\left\{{}\begin{matrix}x+3< 0\\x-2>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< -3\\x>2\end{matrix}\right.\) (vô lý)
Vậy -3<x<2

Ta có 4x + 3 = 4(x - 2) + 11
nên (4x + 3) ⋮ (x - 2) khi 11 ⋮ (x - 2), tức là x -2 là ước của 11
Ư(11) = { -11; -1; 1; 11}; ta có bảng sau:
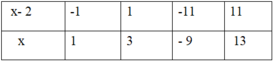
Vậy các số nguyên x thỏa mãn là: x ∈ { 1; 3; - 9; 13}

Lời giải:
$x+10\vdots x+3$
$\Rightarrow (x+3)+7\vdots x+3$
$\Rightarrow 7\vdots x+3$
$\Rightarrow x+3\in \left\{\pm 1; \pm 7\right\}$
$\Rightarrow x\in \left\{-2; -4; 4; -10\right\}$
\(\sqrt[]{}\partial\underrightarrow{ }\sqrt[]{}_{ }\sqrt[]{\begin{matrix}&&\\&&\\&&\end{matrix}}\sqrt{ }\nu\)