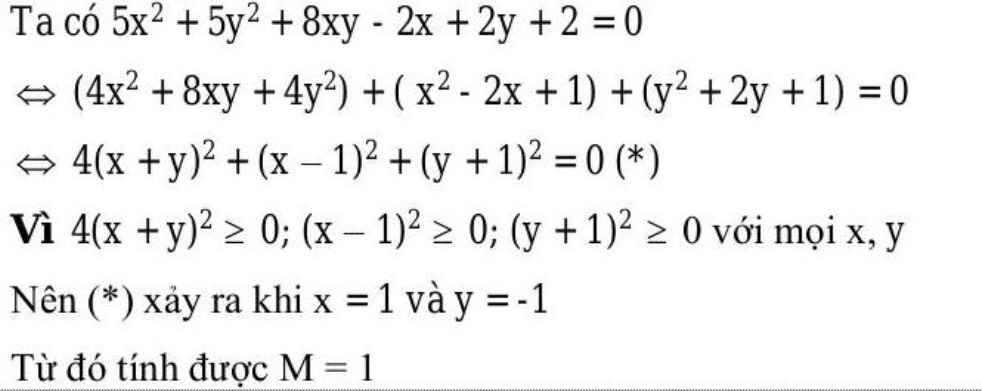2019-2x=2y-2020
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 5x2 + 5y2 + 8xy + 2x - 2y + 2020
A = (4x2 + 8xy + 4y2) + (x2 + 2x + 1) + (y2 - 2y + 1) + 2018
A = 4(x + y)2 + (x + 1)2 + (y - 1)2 + 2018 \(\ge\)2018
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+y=0\\x+1=0\\y-1=0\end{cases}}\)<=> x = -1 và y = 1
Vậy MinA = 2018 khi x = -1 và y = 1
b) B = x2 + 2y2 + 2xy - 2x - 6y + 2019
B = (x + y)2 - 2(x + y) + 1 +(y2 - 4y + 4) + 2014
B = (x + y - 1)2 + (y - 2)2 + 2014 \(\ge\)2014
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+y-1=0\\y-2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=-1\\y=2\end{cases}}\)
Vậy MinB = 2014 khi x = -1 và y = 2
A = 5x2 + 5y2 + 8xy + 2x - 2y + 2020
= ( 4x2 + 8xy + 4y2 ) + ( x2 + 2x + 1 ) + ( y2 - 2y + 1 ) + 2018
= 4( x2 + 2xy + y2 ) + ( x + 1 )2 + ( y - 1 )2 + 2018
= 4( x + y )2 + ( x + 1 )2 + ( y - 1 )2 + 2018 ≥ 2018 ∀ x, y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+y=0\\x+1=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=1\end{cases}}\)
=> MinA = 2018 <=> x = -1 ; y = 1
B = x2 + 2y2 + 2xy - 2x - 6y + 2019
= ( x2 + 2xy + y2 - 2x - 2y + 1 ) + ( y2 - 4y + 4 ) + 2014
= [ ( x2 + 2xy + y2 ) - ( 2x + 2y ) + 1 ] + ( y - 2 )2 + 2014
= [ ( x + y )2 - 2.( x + y ).1 + 12 ] + ( y - 2 )2 + 2014
= ( x + y - 1 )2 + ( y - 2 )2 + 2014 ≥ 2014 ∀ x, y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+y-1=0\\y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=2\end{cases}}\)
=> MinB = 2014 <=> x = -1 ; y = 2


\(5x^2+5y^2+8xy-2x+2y+2=0\)
\(\Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
Vì \(\left(x+y\right)^2\ge0,\left(x-1\right)^2\ge0,\left(y+1\right)^2\ge0\)
\(\Rightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2\ge0\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x+y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(\left(x+y\right)^{2018}+\left(x-2\right)^{2019}+\left(y+1\right)^{2020}=\left(1-1\right)^{2018}+\left(1-2\right)^{2019}+\left(-1+1\right)^{2020}=-1\)

\(y=\dfrac{1}{2x^2+x-1}=\dfrac{1}{\left(x+1\right)\left(2x-1\right)}=\dfrac{2}{3}.\dfrac{1}{2x-1}-\dfrac{1}{3}.\dfrac{1}{x+1}\)
\(y'=\dfrac{2}{3}.\dfrac{-2}{\left(2x-1\right)^2}-\dfrac{1}{3}.\dfrac{-1}{\left(x+1\right)^2}=\dfrac{2}{3}.\dfrac{\left(-1\right)^1.2^1.1!}{\left(2x-1\right)^2}-\dfrac{1}{3}.\dfrac{\left(-1\right)^1.1!}{\left(x+1\right)^2}\)
\(y''=\dfrac{2}{3}.\dfrac{\left(-1\right)^2.2^2.2!}{\left(2x-1\right)^3}-\dfrac{1}{3}.\dfrac{\left(-1\right)^2.2!}{\left(x+1\right)^3}\)
\(\Rightarrow y^{\left(n\right)}=\dfrac{2}{3}.\dfrac{\left(-1\right)^n.2^n.n!}{\left(2x-1\right)^{n+1}}-\dfrac{1}{3}.\dfrac{\left(-1\right)^n.n!}{\left(x+1\right)^{n+1}}\)
\(\Rightarrow y^{\left(2019\right)}=\dfrac{2}{3}.\dfrac{\left(-1\right)^{2019}.2^{2019}.2019!}{\left(2x-1\right)^{2020}}-\dfrac{1}{3}.\dfrac{\left(-1\right)^{2019}.2019!}{\left(x+1\right)^{2020}}\)
\(=\dfrac{2019!}{3}\left(\dfrac{1}{\left(x+1\right)^{2020}}-\dfrac{2^{2020}}{\left(2x-1\right)^{2020}}\right)\)