Bài 2. (1đ) Biểu diễn trên hệ trục tọa độ Oxy: A(1; -2), B(-2; - 1), C(3; -2), D(2; -2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 8 2023
M' đối xứng M qua Ox
=>\(\left\{{}\begin{matrix}x_{M'}=-x_M=1\\y_{M'}=y_M=-2\end{matrix}\right.\)
N' đối xứng N qua Ox
=>\(\left\{{}\begin{matrix}x_{N'}=-x_N=2\\y_{N'}=y_N=-4\end{matrix}\right.\)
P' đối xứng P qua Ox
=>\(\left\{{}\begin{matrix}x_{P'}=-x_P=-2\\y_{P'}=y_P=-3\end{matrix}\right.\)
Q' đối xứng Q qua Ox
=>\(\left\{{}\begin{matrix}x_{Q'}=-x_Q=-3\\y_{Q'}=y_Q=-4,5\end{matrix}\right.\)
28 tháng 2 2022
Bài 3:
a: Thay x=3 vào y=-2x, ta được:
\(y=-2\cdot3=-6\)
b: Thay x=1,5 vào y=-2x, ta được:
\(y=-2\cdot1.5=-3< >3\)
Do đó: B(1,5;3) không thuộc đồ thị hàm số y=2x
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
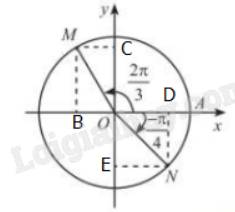
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy; D, E lần lượt là hình chiếu của N lên Ox, Oy
Ta có: OM = ON = 1
\(\widehat{MOC}=\dfrac{2\pi}{3}-\dfrac{\pi}{2}=\dfrac{\pi}{6}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{MOC}=\dfrac{1}{2}\Rightarrow MC=\dfrac{1}{2}\\cos\widehat{MOC}=\dfrac{\sqrt{3}}{2}\Rightarrow MB=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M là \(M\left(-\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\)
\(\widehat{NOD}=-\dfrac{\pi}{4}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{NOD}=-\dfrac{\sqrt{2}}{2}\Rightarrow ND=-\dfrac{\sqrt{2}}{2}\\cos\widehat{NOD}=\dfrac{\sqrt{2}}{2}\Rightarrow NE=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
Vậy tọa độ điểm N là \(N\left(\dfrac{\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)\)
ko biết vì em lớp 5