cho tam giác ABC vuông cân tại A.Gọi M là 1 điểm trên đương cao AH.Chứng Minh Rằng
MB>AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 8 2018
Gọi I là trung điểm của BC
Xét tam giác ABC vuông tại A có AI là đường trung tuyến nên \(AI=\frac{1}{2}BC\)
Theo quan hệ đường xiên và đường vuông góc ta có \(AH\le AI\Rightarrow AH\le\frac{1}{2}BC\)\(\Rightarrow\frac{AH}{BC}\le\frac{1}{2}\)(1)
Ta có \(\frac{S_{AMN}}{S_{ABC}}=\frac{\frac{1}{2}AM.AN}{\frac{1}{2}AH.BC}=\frac{AH^2}{AH.BC}=\frac{AH}{BC}\)(2)
Từ (1) (2) suy ra \(\frac{S_{AMN}}{S_{ABC}}\le\frac{1}{2}\)
26 tháng 4 2020
cho tam giác ABC và 3 điểm A',B',C' lần lượt nằm trên 3 cạnh BC,AC,AB ( A',B',C' không trùng với các đỉnh của tam giác )
Khi đó ta có : AA',BB',CC' đồng quy \(\Leftrightarrow\frac{A'B}{A'C}.\frac{B'C}{B'A}.\frac{C'A}{C'B}=1\)
A B C A' B' C'
26 tháng 4 2020
A B C H E M D P
Gọi P là giao điểm của AD và BE
Áp dụng định lí Ceva vào \(\Delta ABE\),ta có :
\(\frac{BP}{PE}.\frac{HE}{AH}.\frac{AM}{BM}=1\Rightarrow\frac{AH}{HE}=\frac{BP}{PE}\Rightarrow PH//AB\)
\(\Rightarrow\widehat{BAD}=\widehat{DPH}\)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{DAH}=\widehat{PDH}\Rightarrow\Delta AHP\)cân tại H
\(\Rightarrow HP=AH\)
Cần chứng minh \(DP//CE\Leftrightarrow\frac{BD}{BC}=\frac{BP}{BE}\Leftrightarrow\frac{BD}{BC}=1-\frac{EP}{BE}\)
Ta có : \(\frac{EP}{BE}=\frac{HP}{AB}=\frac{AH}{AB}=\frac{HD}{BD}\)
Khi đó : \(\frac{BD}{BC}=1-\frac{HD}{BD}\Leftrightarrow\frac{BD}{BC}+\frac{HD}{BD}=1\Leftrightarrow BD^2+HD.BC=BC.BD=\left(BD+DC\right).BD\)
\(\Rightarrow HD.BC=CD.BD\Rightarrow\frac{HD}{BD}=\frac{CD}{BC}\Leftrightarrow\frac{AH}{AB}=\frac{CD}{BC}\)
Ta có : \(\widehat{CDA}=\widehat{DBA}+\widehat{BAD}=\widehat{CAH}+\widehat{DAH}=\widehat{CAD}\)
\(\Rightarrow\Delta CAD\)cân tại C \(\Rightarrow CD=CA\)
Từ đó suy ra : \(\frac{AH}{AB}=\frac{AC}{BC}\) ( đúng vì \(\Delta AHB~\Delta CAB\left(g.g\right)\))
Vậy ta có đpcm
12 tháng 11 2019
câu a nhá
Có AC và BN là hai đường chéo của tứ giác AHCN
Mà :
MA = MC ( Gt ) thật ra M là trung điểm
BM = NM ( N đối xứng H qua M )
Nên AHCN là hbh có góc H = 90 độ ( AH là đường cao ) vậy hbh AHCN là HCN
CÂU B MK CHƯA HỌC SORRY NHA
KT
29 tháng 3 2018
a) Xét \(\Delta AHB\) và \(\Delta CHA\) có:
\(\widehat{AHB}=\widehat{CHA}=90^0\)
\(\widehat{HAB}=\widehat{HCA}\) do cùng phụ với góc HAC
suy ra: \(\Delta AHB~\Delta CHA\)
\(\Rightarrow\)\(\frac{AH}{CH}=\frac{HB}{HA}\)
\(\Rightarrow\)\(AH^2=HB.CH\)
11 tháng 3 2019
A B C H D E
Ta có:
AB=AD
=> tam giác BDA cân tại B
=> \(\widehat{BAD}=\widehat{BDA}\)(1)
Ta lại có: \(\widehat{BDA}+\widehat{HAD}=90^o,\widehat{BAD}+\widehat{DAE}=90^o\)(2)
Từ (1) và (2) ta suy ra: \(\widehat{HAD}=\widehat{DAE}\)
Xét tam giác HAD và tam giác EAD có:
\(\widehat{HAD}=\widehat{DAE}\)( chứng minh trên)
AH=AE (gt)
AD chung
Suy ra tam giác HAD và tam giác EAD
=> \(\widehat{AHD}=\widehat{ADE}\)
như vậy DE vuông AC
b) Ta có: BD+AH =BA+AE < BA+AC vì (AH=AE, BD=AB, E<AC)
Em xem lại đề bài nhé
KT
cho tam giác ABC vuông tại A đường cao AH .Klaf trung điểm của AH.chứng minh rèn BK vuông góc với AM
1
23 tháng 3 2023
\(\text{#TNam}\)
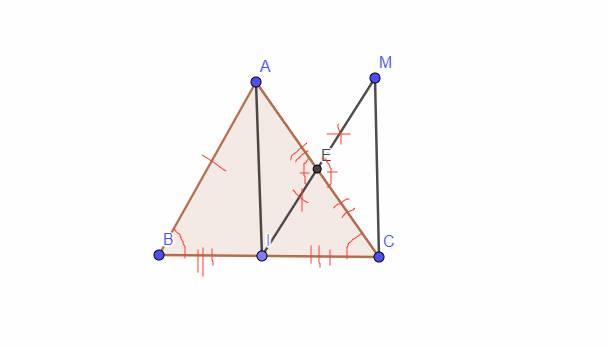
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AIB` và Tam giác `AIC` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`IB = IC (g``t)`
`=> \text {Tam giác AIB = Tam giác AIC (c-g-c)}`
Hnhu câu `b,` bạn ghi thiếu yêu cầu rồi nhé!
`c,` Xét Tam giác `AEI` và Tam giác `MEC` có:
`EA = EC (g``t)`
\(\widehat{AEI}=\widehat{MEC}\) `(\text {2 góc đối đỉnh})`
`EM = EI (g``t)`
`=> \text {Tam giác AEI = Tam giác MEC (c-g-c)}`
`->`\(\widehat{AIE}=\widehat{CME}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong `-> \text {AI // CM}`
Vì Tam giác `ABI =` Tam giác `ACI (a)`
`->`\(\widehat{AIB}=\widehat{AIC}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIB}+\widehat{AIC}=180^0\)
`->`\(\widehat{AIB}=\widehat{AIC}=\) `180/2=90^0`
`-> AI \bot BC`
Mà `\text {AI // CM} -> MC \bot BC`
