a+b=10
Ab-ba=54
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2021
Bạn cần viết đề bằng công thức toán để được hỗ trợ tốt hơn.
22 tháng 11 2017
\(3a^2+3b^2=10ab\)
\(\Rightarrow3a^2-10ab+3b^2=0\)
\(\Rightarrow3a^2-ab-9ab+3b^2=0\)
\(\Rightarrow\left(3a^2-ab\right)-\left(9ab-3b^2\right)=0\)
\(\Rightarrow a\left(3a-b\right)-3b\left(3a-b\right)=0\)
\(\Rightarrow\left(3a-b\right)\left(a-3b\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3a-b=0\\a-3b=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}b=-3a\\b=\dfrac{a}{3}\end{matrix}\right.\)
Với \(b=-3a,\)có :
\(P=\dfrac{-3a-a}{-3a+a}=\dfrac{-4a}{-2a}=2\)
Với \(b=\dfrac{a}{3},\)có :
\(P=\dfrac{\dfrac{a}{3}-a}{\dfrac{a}{3}+a}=\dfrac{\dfrac{a}{3}-\dfrac{3a}{3}}{\dfrac{a}{3}+\dfrac{3a}{3}}=\dfrac{-\dfrac{2a}{3}}{\dfrac{4a}{3}}=-\dfrac{2a}{3}.\dfrac{3}{4a}=-\dfrac{1}{2}\)
( Nếu sai thì cho mk xin lỗi nha bn , tại mk ko chắc lắm )
6 tháng 2 2022
\(3a^2+3b^2=10ab\)
\(\Leftrightarrow3a^2-10ab+3b^2=0\)
\(\Rightarrow3a^2-9ab-ab+3b^2=0\)
\(\Leftrightarrow3a\left(a-3b\right)-b\left(a-3b\right)=0\)
\(\Leftrightarrow\left(a-3b\right)\left(3a-b\right)=0\)
Trường hợp 1: a=3b
\(A=\dfrac{a-b}{a+b}=\dfrac{3b-b}{3b+b}=\dfrac{2}{4}=\dfrac{1}{2}\)
Trường hợp 2: b=3a
\(A=\dfrac{a-b}{a+b}=\dfrac{a-3a}{a+3a}=\dfrac{-2}{4}=-\dfrac{1}{2}\)
10 tháng 7 2023
3(a^2+b^2)=10ab
=>3a^2-10ab+3b^2=0
=>3a^2-9ab-ab+3b^2=0
=>3a(a-3b)-b(a-3b)=0
=>(a-3b)(3a-b)=0
=>b=3a(loại) hoặc a=3b(nhận)
\(K=\dfrac{3b+b}{3b-b}=2\)
CM
23 tháng 3 2019
Ta có 9 a 2 + b = 10 a b ⇔ 3 a + b 4 2 = a b
Suy ra
log 3 a + b 4 = log a b ⇔ log 3 a + b 4 = log a + log b 2
Đáp án B
CM
5 tháng 12 2019
Điều kiện xác định của phân thức: a ≠ 0, b ≠ 0 , b ≠ a/2
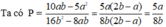
Với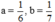 
thỏa mãn điều kiện xác định của phân thức
CM
27 tháng 5 2017
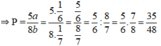
Điều kiện xác định của phân thức: a ≠ 0, b ≠ 0 , b ≠ a/2
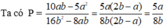
Với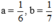 
thỏa mãn điều kiện xác định của phân thức
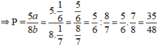
Ta có:ab-ba=54
=>(10a+b)-(10b+a)=54
=>10a+b-10b-a=54
=>9a-9b=54=>9(a-b)=54=>a-b=6
Do đó a>b
Mà a+b=10
=>a=(10+6):2=8
=>b=(10-6):2=2
Vậy ...