Giúp bài 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PP
bài 6 giúp mk nha
2
DP
0
DV
3
25 tháng 2 2022
Bài 6:
a, Sxq = ( 0,6+ 0,3) x 2 x 0,4 = 0,72 (m2)
Stp= 0,72 + 0,6x0,3x2 =1,08(m2)
V = 0,6 x0,3 x 0,4 = 0,072 (m3)
b, Đổi 3dm= 0,3 m
Sxq=(1/2 + 1/5 ) x 2 x 0,3= 0,42(m2)
Stp= 0,42 + 1/2 x 1/5 x 2 = 0,62(m2)
V= 1/2 x 1/5 x 0,3 =0,03(m3)
25 tháng 2 2022
a,S xung quanh HHCN là :
2,0,4,(0,6+0,3)=0,98(m2)
S toàn phần HHCN là :
0,98+2.0,6.0,3=1,34(m2)
Thể tích HHCN là :
0,6.0,3.0,4=0,072(m3)
b,Đổi 3dm=0,3m
S xung quanh HHCN là :
2.0,3.(1/2+1/5)=21/50(m2)
S toàn phần HHCN là :
21/50+2.1/2.1/5=31/50(m2)
Thể tích HHCN là :
1/5.0,3.1/2=3/100(m3)
_HT_
M
3
10 tháng 3 2021
1: Nhận thấy x = 0 không là nghiệm của pt.
Chia cả hai vế của pt cho x2 ta được:
\(x^2+5x-12+\dfrac{5}{x}+\dfrac{1}{x^2}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+5\left(x+\dfrac{1}{x}\right)-14=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}-2\right)\left(x+\dfrac{1}{x}+7\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{x}=2\\x+\dfrac{1}{x}=-7\end{matrix}\right.\).
Với \(x+\dfrac{1}{x}=2\Rightarrow x^2-2x+1=0\Leftrightarrow x=1\) (thoả mãn x khác 0)
Với \(x+\dfrac{1}{x}=-7\Rightarrow x^2+7x+1=0\Leftrightarrow x=\dfrac{\pm\sqrt{45}-7}{2}\) (thoả mãn x khác 0)
Vậy...
CL
giải giúp mik đề 4
1
TT
2
12 tháng 11 2021
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a-b}{6-4}=\dfrac{30}{2}=15\)
Do đó: a=90; b=60; c=45
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
Bài 6:
\(a,2x^2y^2\left(x^3y^2-x^2y^3-\dfrac{1}{2}y^5\right)=2x^2y^2.x^3y^2-2x^2y^2.x^2y^3-2.x^2y^2.\dfrac{1}{2}y^5\\ =2x^5y^4-2x^4y^5-x^2y^7\\ b,-\dfrac{1}{3}xy\left(3x^2y^2-6x^2+y^2\right)\\ =-\dfrac{1}{3}.3.x.x^2.y.y^2-\dfrac{1}{3}.\left(-6\right)x.x^2.y-\dfrac{1}{3}x.y.y^2=-x^3y^3+2x^3y-\dfrac{1}{3}xy^3\\ c,\left(-2xy^2+\dfrac{2}{3}y^2+4xy^2\right).\dfrac{3}{2}xy=-2.\dfrac{3}{2}x.x.y.y^2+\dfrac{2}{3}.\dfrac{3}{2}xy.y^2+4.\dfrac{3}{2}x.x.y^2.y\\ =-3x^2y^3+xy^3+6x^2y^3=3x^2y^3+xy^3\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
Bài 6:
\(d,x^2+2xy-3\left(-xy\right)=x^2+2xy+3xy=x^2+5xy\\ e,\dfrac{1}{2}x^2y\left(2x^3-\dfrac{2}{5}x.y^2-1\right)=\dfrac{1}{2}.2.x^2.x^3.y-\dfrac{1}{2}.\dfrac{2}{5}.x^2y.x.y^2-\dfrac{1}{2}x^2y\\ =x^5y-\dfrac{1}{5}x^3y^3-\dfrac{1}{2}x^2y\\ f,\left(-xy^2\right)^2.\left(x^2-2x+1\right)=\left(xy^2\right)^2.\left(x-1\right)^2=\left[xy^2.\left(x-1\right)\right]^2\\ =\left(x^2y^2-xy^2\right)^2\)
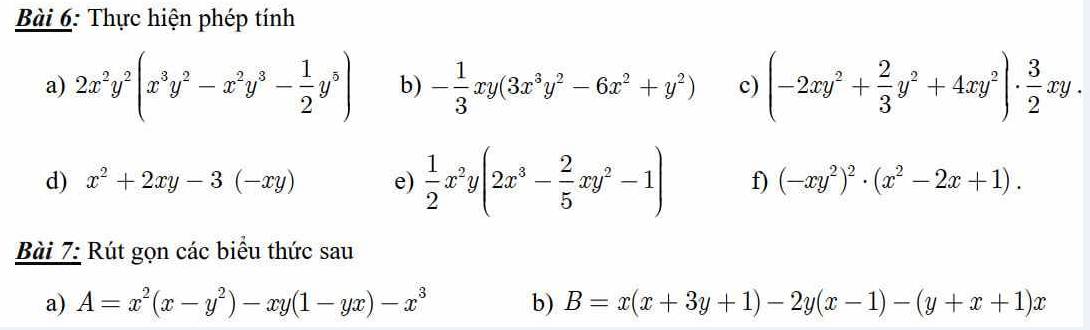
a) Xét tam giác ABE và KBE có :
BE-cạnh chung
\(\widehat{ ABE}=\widehat{EBK}\left(gt\right)\)
\(\widehat{BEA}=\widehat{BEK}=90^o\)
=> Tg ABE=KBE(g.c.g)
=> AB=AK
=> Tg ABK cân tại B (đccm)
b) Xét tg ABD và KBD có :
BD-cạnh chung
\(\widehat{ABD}=\widehat{KBD}\left(gt\right)\)
AB=AK(cmt)
=> Tg ABD=KBD(c.g.c)
\(\Rightarrow\widehat{BAD}=\widehat{BKD}=90^o\)
\(\Rightarrow KD\perp BC\)(đccm)
c) Có : \(\widehat{AHC}=\widehat{DKC}=90^o\)
=> AH//KC
\(\Rightarrow\widehat{AKD}=\widehat{KAH}\left(1\right)\)
- Do tg BAD=BKD(cmt)
=> AD=DK
=> Tg AKD cân tại D
\(\Rightarrow\widehat{KAD}=\widehat{AKD}\left(2\right)\)
- Từ (1) và (2)\(\Rightarrow\widehat{HAK}=\widehat{KAD}\)
=> AK là tia pgiac góc HAC (đccm)
#H