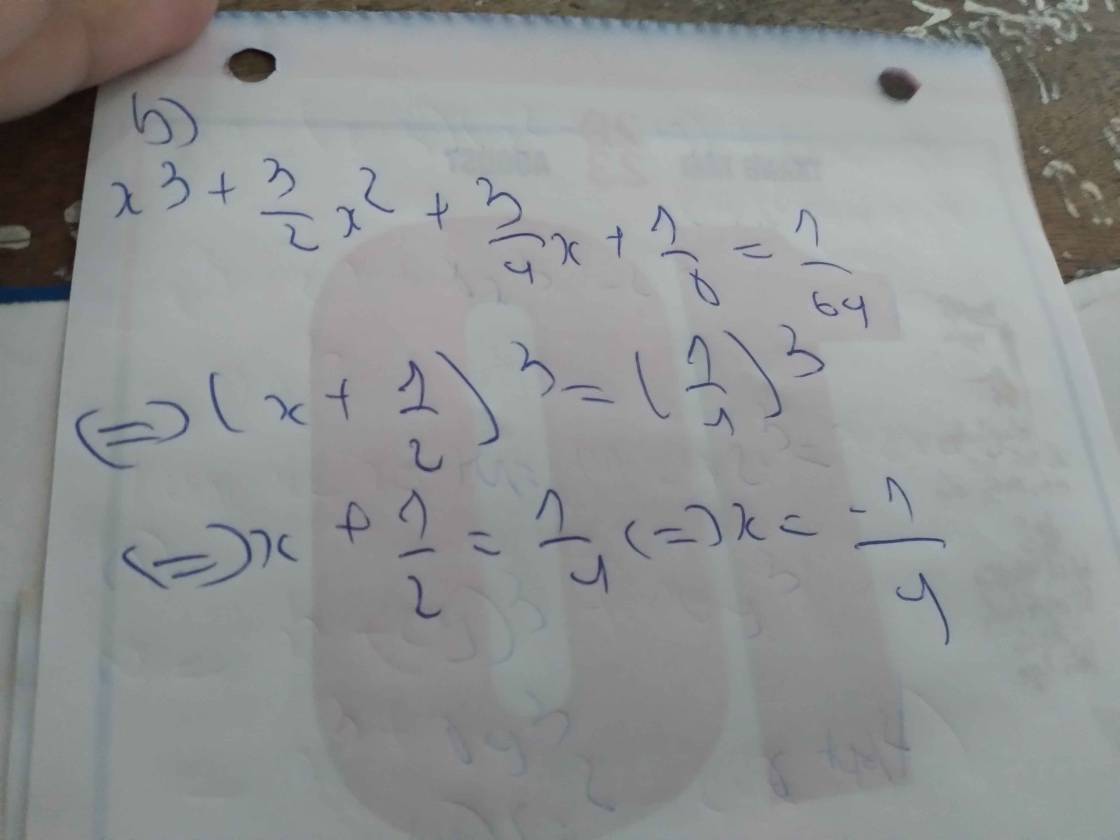(4x-1)^3=64^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
2
12 tháng 8 2023
\(\left(x-3\right)=\left(3-x\right)^2\)
\(\Leftrightarrow x-3=\left(x-3\right)^2\)
\(\Leftrightarrow\left(x-3\right)-\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x-3\right)\left[1-\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x-3\right)\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\4-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
___________
\(x^3+\dfrac{3}{2}x^2+\dfrac{3}{4}x+\dfrac{1}{8}=\dfrac{1}{64}\)
\(\Leftrightarrow x^3+3\cdot\dfrac{1}{2}\cdot x^2+3\cdot\left(\dfrac{1}{2}\right)^2\cdot x+\left(\dfrac{1}{2}\right)^3=\dfrac{1}{64}\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^3=\left(\dfrac{1}{4}\right)^3\)
\(\Leftrightarrow x+\dfrac{1}{2}=\dfrac{1}{4}\)
\(\Leftrightarrow x=\dfrac{1}{4}-\dfrac{1}{2}\)
\(\Leftrightarrow x=-\dfrac{1}{4}\)
TN
21 tháng 6 2017
\(\left(\dfrac{1}{2}x+5\right)^3=\dfrac{1}{8}x^3+\dfrac{15}{4}x^2+\dfrac{75}{2}x+25\)
\(8x^3+\dfrac{1}{64}=\left(2x+\dfrac{1}{4}\right)\left(4x^2-\dfrac{1}{2}x+\dfrac{1}{16}\right)\)\(\left(4x-\dfrac{1}{2}\right)^3=64x^3-24x^2+3x-\dfrac{1}{8}\)
LT
2
25 tháng 7 2018
+) \(\left(x-3\right)^2=16\)
\(\Rightarrow\orbr{\begin{cases}\left(x-3\right)^2=4^2\\\left(x-3\right)^2=\left(-4\right)^2\end{cases}\Rightarrow}\orbr{\begin{cases}x-3=4\\x-3=-4\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=-1\end{cases}}\)
Vậy x = 7 hoặc x = -1
+) \(\left(1-3x\right)^3=-64\)
\(\Rightarrow\left(1-3x\right)^3=\left(-4\right)^3\)
\(\Rightarrow1-3x=-4\)
\(\Rightarrow3x=1+4\)
\(\Rightarrow3x=5\)
\(\Rightarrow x=5:3\)
\(\Rightarrow x=\frac{5}{3}\)
Vậy \(x=\frac{5}{3}\)
+) \(x^{13}=27.x^{10}\)
\(\Rightarrow x^{13}:x^{10}=27\)
\(\Rightarrow x^3=27\)
\(\Rightarrow x^3=3^3\)
\(\Rightarrow x=3\)
Vậy x = 3
+) \(\left(4x-1\right)^2=\left(1-4x\right)^4\)
\(\Rightarrow\left(4x-1\right)^2=\left(4x-1\right)^4\)
\(\Rightarrow\left(4x-1\right)^2-\left(4x-1\right)^4=0\)
\(\Rightarrow\left(4x-1\right)^2\left[1-\left(4x-1\right)^2\right]=0\)
\(\Rightarrow\orbr{\begin{cases}\left(4x-1\right)^2=0\\1-\left(4x-1\right)^2=0\end{cases}}\Rightarrow\orbr{\begin{cases}\left(4x-1\right)^2=0\\\left(4x-1\right)^2=1\end{cases}}\)
TH 1 : \(\left(4x-1\right)^2=0\Rightarrow4x-1=0\Rightarrow4x=1\Rightarrow x=\frac{1}{4}\)
TH 2 : \(\left(4x-1\right)^2=1\Rightarrow\orbr{\begin{cases}4x-1=1\\4x-1=-1\end{cases}}\Rightarrow\orbr{\begin{cases}4x=2\\4x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=0\end{cases}}\)
Vậy \(x\in\left\{\frac{1}{4};\frac{1}{2};0\right\}\)
_Chúc bạn học tốt_
25 tháng 7 2018
a, (x-3)^2 = 16
=> (x-3)^2=4^2
=> x-3=4
=> x= 4+3
=> x = 7 .Vậy x =7
b,(1-3x)^3 = 64
=> ( 1-3x)^3 = 4^3
=> 1-3x = 4
=> 3x = 1-4
=> 3x = -3
=> x = -1 . Vậy x = -1
c, x^13 = 27.x^10
=> x^13 : x^10 = 27
=> x^3 = 3^3
=> x = 3 . Vậy x = 3
5 tháng 7 2018
a) 4x2+4x+1
= (2x+1)2
b) x2-16x+64
= (x-8)2
c) 4x2-9y2
= (2x+3y)(2x-3y)
d) ( x-3).(x^2+3x+9)
11 tháng 7 2023
\(M=\left(7-2x\right)\left(4x^2+14x+49\right)-\left(64-8x^3\right)\)
\(M=\left(7-2x\right)\left[\left(2x\right)^2+2x\cdot7+7^2\right]-\left(64-8x^3\right)\)
\(M=\left[7^3-\left(2x\right)^3\right]-\left(64-8x^3\right)\)
\(M=343-8x^3-64+8x^3\)
\(M=279\)
Vậy M có giá trị 279 với mọi x
\(P=\left(2x-1\right)\left(4x^2-2x+1\right)-\left(1-2x\right)\left(1+2x+4x^2\right)\)
\(P=8x^3-4x^2+2x-4x^2+2x-1-1+8x^3\)
\(P=16x^3-8x^2+4x-2\)
Thay \(x=10\) vào P ta có:
\(P=16\cdot10^3-8\cdot10^2+4\cdot10-2=15238\)
Vậy P có giá trị 15238 tại x=10
10 tháng 7 2023
a: M=343-8x^3-64+8x^3=279
b: P=8x^3-4x^2+2x-4x^2+2x-1-1+8x^3
=16x^3-8x^2+4x-2
=16*10^3-8*10^2+4*10-2=15238
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
1.
$\sqrt{3x^2}-\sqrt{12}=0$
$\Leftrightarrow \sqrt{3x^2}=\sqrt{12}$
$\Leftrightarrow 3x^2=12$
$\Leftrightarrow x^2=4$
$\Leftrightarrow (x-2)(x+2)=0\Leftrightarrow x=\pm 2$
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
2.
$\sqrt{(x-3)^2}=9$
$\Leftrightarrow |x-3|=9$
$\Leftrightarrow x-3=9$ hoặc $x-3=-9$
$\Leftrightarrow x=12$ hoặc $x=-6$
TM
1
13 tháng 2 2018
\(\sqrt{2x^2+4x-1}=\sqrt{2\left(x+\dfrac{2-\sqrt{6}}{2}\right)\left(x+\dfrac{2+\sqrt{6}}{2}\right)}\)
\(\Rightarrow\) BXD :
| \(x\) | \(-\infty\) | \(\dfrac{-2-\sqrt{6}}{2}\) | \(\dfrac{-2+\sqrt{6}}{2}\) | \(+\infty\) | ||||
| \(x+\dfrac{2-\sqrt{6}}{2}\) | \(-\) | \(-\) | \(-\) | \(-\) | \(0\) | \(+\) | \(+\) | |
| \(x+\dfrac{2+\sqrt{6}}{2}\) | \(-\) | \(-\) | \(0\) | \(+\) | \(+\) | \(+\) | \(+\) | |
| \(\sqrt{2x^2+4x-1}\) | \(+\) | \(+\) | \(0\) | oxđ | \(0\) | \(+\) | \(+\) |
\(\Rightarrow\) \(\sqrt{2x^2+4x-1}\) xác định \(\Leftrightarrow x\in\left(-\infty;\dfrac{-2-\sqrt{6}}{2}\right)\cup\left(\dfrac{-2+\sqrt{6}}{2};+\infty\right)\)
ta có : \(\sqrt{2x^2+4x-1}>x+1\)
\(\Leftrightarrow\sqrt{2x^2+4x-1}-x-1>0\)
\(\Rightarrow\) BXD :
| \(x\) | \(-\infty\) | \(\dfrac{-2-\sqrt{6}}{2}\) | \(-1\) | \(\dfrac{-2+\sqrt{6}}{2}\) | \(+\infty\) | ||||
| \(\sqrt{2x^2+4x-1}\) | \(+\) | \(+\) | \(0\) | oxđ | oxđ | oxđ | \(0\) | \(+\) | |
| \(-x-1\) | \(+\) | \(+\) | \(\dfrac{\sqrt{6}}{2}\) | bỏ | \(0\) | bỏ | \(\dfrac{-\sqrt{6}}{2}\) | \(-\) | |
| \(f\left(x\right)\) | \(+\) | \(+\) | \(0\) | bỏ | bỏ | \(0\) | không rỏ dấu |
bn nào giỏi lm tiếp đi nha
HH
2
7 tháng 9 2021
a) \(x^2-64=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
b) \(4x^2-4x+1=0\)
\(\Leftrightarrow\left(2x-1\right)^2=0\Leftrightarrow2x-1=0\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
c) \(9-6x+x^2=0\)
\(\Leftrightarrow\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\Leftrightarrow x=3\)
7 tháng 9 2021
a: Ta có: \(x^2-64=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
b: Ta có: \(4x^2-4x+1=0\)
\(\Leftrightarrow\left(2x-1\right)^2=0\)
hay \(x=\dfrac{1}{2}\)
c: ta có: \(x^2-6x+9=0\)
\(\Leftrightarrow\left(x-3\right)^2=0\)
hay x=3
HL
2
17 tháng 8 2023
\(318-5\left(x-64\right)=103\)
\(\Rightarrow5\left(x-64\right)=318-103\)
\(\Rightarrow5\left(x-64\right)=215\)
\(\Rightarrow x-64=43\)
\(\Rightarrow x=43+64\)
\(\Rightarrow x=107\)
_____________
\(4^x\cdot5+216=296\)
\(\Rightarrow4^x\cdot5=296-216\)
\(\Rightarrow4^x\cdot5-80\)
\(\Rightarrow4^x=16\)
\(\Rightarrow4^x=4^2\)
\(\Rightarrow x=2\)
___________
\(376-6^x:3=364\)
\(\Rightarrow6^x:3=376-364\)
\(\Rightarrow6^x:3=12\)
\(\Rightarrow6^x=36\)
\(\Rightarrow6^x=6^2\)
\(\Rightarrow x=2\)
___________
\(\left(4x-1\right)^2=121\)
\(\Rightarrow\left(4x-1\right)^2=11^2\)
\(\Rightarrow\left[{}\begin{matrix}4x-1=11\\4x-1=-11\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}4x=12\\4x=-10\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)