K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2023
5:
d: \(A=\dfrac{9\left(x_1+x_2\right)+10-3m}{18\left(x_1x_2+2\right)^2+1}\)
\(=\dfrac{9\cdot\dfrac{m-2}{3}+10-3m}{18\cdot\left(\dfrac{m-6}{3}+2\right)^2+1}=\dfrac{3m-6+10-3m}{18\cdot\left(\dfrac{m-6+6}{3}\right)^2+1}\)
\(=\dfrac{4}{18\cdot\dfrac{m^2}{9}+1}=\dfrac{4}{2m^2+1}< =\dfrac{4}{1}=4\)
Dấu = xảy ra khi m=0
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
A
0
LN
0
LN
18 tháng 10 2021
Bác mẹ là chỉ cha mẹ
Hai thân vui vầy là cha mẹ vui vẻ, hạnh phúc.
Mình biết vậy thui mong có ích cho bạn!
18 tháng 10 2021
bạn viết cho mình là mình vui rồi ! Cảm ơn bạn nhé !
BN
1
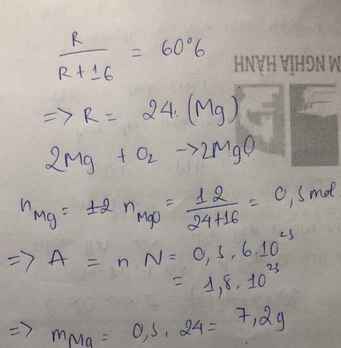
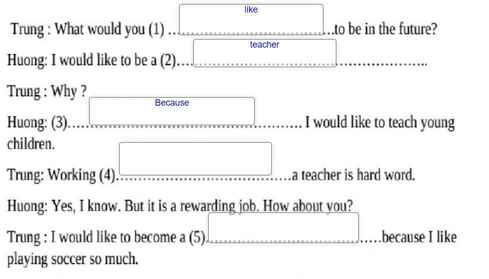
Hơi mờ, lần sau bạn nên gõ Tex nhìn dễ hơn nhé
Ta có: \(A=x^2\left(x-2\right)^2+\left(x-2\right)^2+\left(y-5\right)^4+7\)
\(A=\left(x^2+1\right)\left(x-2\right)^2+\left(y-5\right)^4+7\)
\(\ge\left(x^2+1\right)\cdot0+0+7=7\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}\left(x-2\right)^2=0\\\left(y-5\right)^2=0\end{cases}}\Rightarrow\hept{\begin{cases}x=2\\y=5\end{cases}}\)
Vậy Min(A) = 7 khi \(\hept{\begin{cases}x=2\\y=5\end{cases}}\)
ta có: \(^{x^2\left(x-2\right)^2\ge0}\)
\(\left(x-2\right)^2\ge0\)
\(\left(y-5\right)^4\ge0\)
\(\Rightarrow x^2\left(x-2\right)^2+\left(x-2\right)^2+\left(y-5\right)^4+7\ge7\)
vậy Min A = 7 khi x=2 và y = - 5