Tìm x biết:
\(x^2 + 5x + {\sqrt{x^2+5x +30}}=12\)
Giúp mình với !!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(3x^2+5x-3\right)+\left(x-3x^2-3\right)=0\)
\(\Leftrightarrow6x-6=0\)
\(\Leftrightarrow6x=6\Leftrightarrow x=1\)
b) \(\left(3x^2-5x\right)-\left(3x^2+x-12\right)=0\)
\(\Leftrightarrow3x^2-5x-3x^2-x+12=0\)
\(\Leftrightarrow-6x=-12\Leftrightarrow x=2\)

a) (5x - 12 ) : 4 = 318 : 315
( 5x - 12 ) : 4 = 33
( 5x - 12 ) : 4 = 27
5x - 12 = 108
5x = 120
x = 24
b) 5x3 - 102 = 35
5x3 - 100 = 35
5x3 = 135
x3 = 27
x3 = 33
=> x = 3
c) 65 - 4x+2 = 20180
65 - 4x+2 = 1
4x+2 = 64
4x+2 = 43
x + 2 = 3
=> x = 1
d) 2x+1 - 2x = 32
2x . ( 2 - 1 ) = 32
2x . 1 = 32
2x = 32
2x = 25
=> x = 5

a) \(x^2-5x+6\)
\(=x^2-2x-3x+6=x\left(x-2\right)-3\left(x-2\right)=\left(x-2\right)\left(x-3\right)\)
b) \(x^2-9x+18=x^2-3x-6x+18\)
\(=x\left(x-3\right)-6\left(x-3\right)=\left(x-3\right)\left(x-6\right)\)
c) \(x^2-6x+5=x^2-x-5x+5\)
\(=x\left(x-1\right)-5\left(x-1\right)=\left(x-1\right)\left(x-5\right)\)
d) \(3x^2+5x-30=3\left(x^2+\dfrac{5x}{3}-10\right)=3\left(x^2+2.x.\dfrac{5}{6}+\dfrac{25}{36}-\dfrac{5347}{500}\right)\)
Câu này bạn xem lại đề nha
e) \(3x^2-5x-2=3x^2-6x+x-2\)
\(3x\left(x-2\right)+x-2=\left(x-2\right)\left(3x+1\right)\)

a, x - 3 : 2 = 5 14 : 5 12
=> x - 3 : 2 = 5 2
=> x - 3 : 2 = 25
=> x – 3 = 25
=> x = 53
b, 30 : x - 7 = 15 19 : 15 18
=> 30 : x - 7 = 15
=> x – 7 = 2
=> x = 9
c, x 70 = x
=> x 70 - x = 0
=> x ( x 69 - 1 ) = 0
=> 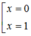
d, 2 x + 1 3 = 9 . 81
=> 2 x + 1 3 = 9 3
=> 2x + 1 = 9
=> x = 4
e, 5 x + 5 x + 2 = 650
=> 5 x 1 + 5 2 = 650
=> 5 x . 26 = 650
=> 5 x = 25
=> x = 2
f, 4 x - 1 2 = 25 . 9
=> 4 x - 1 2 = 5 2 . 3 2
=> 4 x - 1 2 = 15 2
=> 4x – 1 = 15
=> x = 4

Ta có
(\(\sqrt{x^2-5x+14}+\sqrt{x^2-5x+10}\))(\(\sqrt{x^2-5x+14}-\sqrt{x^2-5x+10}\)) = 4
=> M = 2
Đk: \(\forall\)x \(\in\)R
\(x^2+5x+\sqrt{x^2+5x+30}=12\)
<=> \(x^2+5x+30+\sqrt{x^2+5x+30}-42=0\)
Đặt \(\sqrt{x^2+5x+30}=a\)(a > 0) <=> \(x^2+5x+30=a^2\)
Khi đó, ta có: \(a^2+a-42=0\)
<=> \(a^2+7a-6b-42=0\)
<=> \(\left(a-6\right)\left(a+7\right)=0\)
<=> \(\orbr{\begin{cases}a=6\left(tm\right)\\a=-7\left(ktm\right)\end{cases}}\)
<=> \(\sqrt{x^2+5x+30}=6\)
<=> \(x^2+5x+30=36\)
<=> \(x^2+5x-6=0\)
<=> \(x^2+6x-x-6=0\)
<=> \(\left(x+6\right)\left(x-1\right)=0\)
<=> \(\orbr{\begin{cases}x=-6\\x=1\end{cases}}\)
Vậy S = {-6; 1}
\(ĐKXĐ:x\inℝ\)
\(x^2+5x+\sqrt{x^2+5x+30}=12\)
\(\Leftrightarrow x^2+5x+30+\sqrt{x^2+5x+30}=42\)
\(\Leftrightarrow\left(x^2+5x+30\right)+\sqrt{x^2+5x+30}-42=0\)(1)
Đặt \(\sqrt{x^2+5x+30}=a\)( \(a\ge0\))
\(\Rightarrow x^2+5x+30=a^2\)
Từ (1) \(\Rightarrow a^2+a-42=0\)
\(\Leftrightarrow a^2-6a+7a-42=0\)
\(\Leftrightarrow a\left(a-6\right)+7\left(a-6\right)=0\)
\(\Leftrightarrow\left(a-6\right)\left(a+7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a-6=0\\a+7=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}a=6\\a=-7\end{cases}}\)
\(\Rightarrow a=-7\)loại vì \(a\ge0\)
\(\Rightarrow a=6\)\(\Leftrightarrow\sqrt{x^2+5x+30}=6\)
\(\Leftrightarrow x^2+5x+30=36\)\(\Leftrightarrow x^2+5x-6=0\)
\(\Leftrightarrow x^2-x+6x-6=0\)\(\Leftrightarrow x\left(x-1\right)+6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+6\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+6=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-6\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{1;-6\right\}\)