Giải và biện luận phương trình: (2m+3)x+7=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MS
0
CM
23 tháng 1 2017
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
LK
2
NN
18 tháng 1 2016
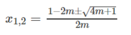
với 2m-1 bằng 0 thì => m=1/2 => pt -3=5( vô lý)
với 2m-1 khác 0 => m khác 1/2 => pt (2m-1)x = 8
=> x = 8/(2m-1)
vậy với m= 1/2 pt vô nghiệm
với m khác 1/2 thì phương trình có nghiệm duy nhất là x=8/(2m-1)
18 tháng 1 2016
2mx-x-3=5
<=> x(2m-1)=8
+, với m khác 1/2 thì phương trình có nghiệm duy nhất là x= 8/(2m-1)
+, với m=1/2 thì x.0=8 (1)
<=> phương trình (1) vô nghiệm
<=> phuong trình đã cho vô nghiệm
TN
0
HV
1
17 tháng 11 2021
\(\left(m^2-3\right)x-2m^2=x-4m\)
\(\Leftrightarrow\left(m^2-4\right)x=2m^2-4m\)
\(\Leftrightarrow\left(m-2\right)\left(m+2\right)x=2m\left(m-2\right)\)
Với m = 2 PT luôn đúng với mọi x
Với m = -2 PT không có nghiệm số thực
Với \(m\ne2\)và \(-2\)ta có :
\(x=\frac{2m}{m+2}\)
CM
22 tháng 8 2019
(2m + 1)x – 2m = 3x – 2
⇔ (2m + 1)x – 3x = 2m – 2
⇔ (2m + 1 – 3).x = 2m – 2
⇔ (2m – 2).x = 2m – 2 (3)
+ Xét 2m – 2 ≠ 0 ⇔ m ≠ 1, pt (3) có nghiệm duy nhất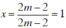 
+ Xét 2m – 2 = 0 ⇔ m = 1, pt (3) ⇔ 0.x = 0, phương trình có vô số nghiệm.
Kết luận :
+ Với m = 1, phương trình có vô số nghiệm
+ Với m ≠ 1, phương trình có nghiệm duy nhất x = 1.
\(\Leftrightarrow\left(2m+3\right)x=-7\) (1)Nếu 2m + 3 = 0
\(\Leftrightarrow m=-\dfrac{3}{2}\)
\(\left(1\right)\Leftrightarrow0=-7\) (vô lí)=> Pt vô nghiệm
Nếu \(2m+3\ne0\)
\(\Leftrightarrow m\ne-\dfrac{3}{2}\)
\(\left(1\right)\Leftrightarrow x=-\dfrac{7}{2m+3}\)
Vậy :
Với \(m=-\dfrac{3}{2}\), phương trình đã cho vô nghiệm
Với \(m\ne-\dfrac{3}{2}\), phương trình đã cho có nghiệm duy nhất là \(x=-\dfrac{7}{2m+3}\)