Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng định lý Pytago vào tam giác ABC, ta có
AB2+AC2=BC2
=>36 + 64 = BC2
=>BC=10cm
Chu vi tam giác ABC là:
6+8+10=24cm

a) Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E
có: BD là cạnh chung
góc ABD = góc EBD (gt)
\(\Rightarrow\Delta ABD=\Delta EBD\left(ch-gn\right)\)
b) ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AB = EB = 6 cm ( 2 cạnh tương ứng)
=> EB = 6 cm
Xét tam giác ABC vuông tại A
có: \(AB^2+AC^2=BC^2\left(py-ta-go\right)\)
thay số: \(6^2+8^2=BC^2\)
\(\Rightarrow BC^2=100\)
\(\Rightarrow BC=10cm\)
mà \(E\in BC\)
=> EB + EC = BC
thay số: 6 + EC = 10
EC = 10 - 6
=> EC = 4 cm
c) ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AD = ED ( 2 cạnh tương ứng)
AB = EB ( 2 cạnh tương ứng) (1)
Xét tam giác ADI vuông tại A và tam giác EDC vuông tại E
có: AD = ED ( chứng minh trên)
góc ADI = góc EDC ( đối đỉnh)
\(\Rightarrow\Delta ADI=\Delta EDC\left(cgv-gn\right)\)
=> AI = EC ( 2 cạnh tương ứng)(2)
Từ (1);(2) => AB + AI = EB + EC
=> BI = BC
=> tam giác BIC cân tại B ( định lí tam giác cân)
d) ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AD = ED ( 2 cạnh tương ứng) (1)
Xét tam giác EDC vuông tại E
có: ED < DC ( định lí cạnh góc vuông, cạnh huyền) (2)
Từ (1);(2) => AD <DC
mk ko bít kẻ hình trên này!
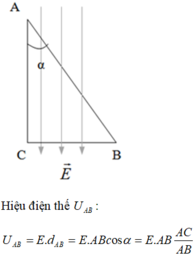

\(\overrightarrow{A_{AC}}=q.\overrightarrow{E_{AC}}.\overrightarrow{AC}\Rightarrow A_{AC}=-1,6.10^{-19}.3000.0,08=...\left(J\right)\)
\(\overrightarrow{A_{BC}}=q.\overrightarrow{E_{BC}}.\overrightarrow{BC}=-1,6.10^{-19}.3000.0,06.\cos90^0=...\left(J\right)\)