Cho tam giác ABC, gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC; và M, N, P, Q theo thứ tự là trung điểm các đoạn thẳng DA, AE, EF, FD
a) Chứng minh: EF là đường trung bình của tam giác ABC
b) Chứng minh: Các tứ giác DAEF; MNPQ là hình bình hành
c) Khi tam giác ABC vuông tại A thì các tứ giác DAEF; MNPQ là hình gì ? Chứng minh?

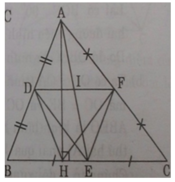


A B C D F E M N Q P O I
Bài làm
a) Xét tam giác ABC có:
E là trung điểm AC
F là trung điểm BC
=> EF là đường trung bình
Vậy EF là đường trung bình của tam giác ABC (đpcm)
b) Vì EF là đường trung bình của tam giác ABC
=> EF // AB => EF // AD
=> EF = 1/2AB.
Mà AD = 1/2AB (Do D là trung điểm AB)
=> EF = AD
Xét tứ giác ADEF có:
EF // AD (chứng minh trên)
EF = AD (chứng minh trên)
=> Tứ giác ADEF là hình bình hành.
Nối AF
Xét tam giác EAF có:
N là trung điểm AE
P là trung điểm EF
=> NP là đường trung bình của tam giác EAF
=> NP = 1/2AF (1)
=> NP // AF (2)
Xét tam giác DAF có:
M là trung điểm AD
Q là trung điểm DF
=> MQ là đường trung bình của tam giác DAF
=> MQ = 1/2AF (3)
=> MQ // AF (4)
Từ (1) và (3) => NP = MQ
Từ (2) và (4) => MQ // NP
Xét tứ giác MNPQ có:
NP = MQ (chứng minh trên)
NP // MQ (chứng minh trên)
=> MNPQ là hình bình hành.
c) Nếu tam giác ABC vuông tại A
=> \(\widehat{BAC}=90^0\)
Mà tứ giác DAEF là hình bình hành (theo câu b)
=> DAEF là hình chữ nhật.
Vì DAEF là hình chữ nhật
=> AF vuông góc DE (tính chất hai đường chéo)
Gọi giao điểm của AF và DE là O
=> AF vuông góc với DE tại O
Gọi giao điểm của DE với NP là I
Xét tam giác AEO vuông tại O có:
N là trung điểm AE
NI // AO (Do NP // AF chứng minh ở trên)
=> NI là đường trung bình
=> NI // AO
Mà \(\widehat{AOE}\)và \(\widehat{NIO}\)trong cùng phía bù nhau
=> \(\widehat{NIO}=90^0\)
Xét tam giác AED có:
M là trung điểm AD
N là trung điểm AE
=> MN là đường trung bình
=> MN // DE
Mà \(\widehat{MNI}+\widehat{NIO}=180^0\)(trong cùng phía)
hay \(\widehat{MNP}=180^0-90^0\)
=> \(\widehat{MNP}=90^0\)
Mà tứ giác MNPQ là hình bình hành
=> MNPQ là hình chữ nhật.