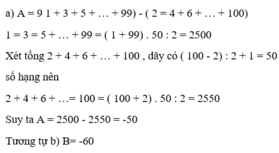Tính tổng: A= 1+ 2^2+ 2^3+ 2^4+.......+2^20.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 10 2023
5:
a: \(3^{2n}=\left(3^2\right)^n=9^n\)
\(\left(2^{3n}\right)=\left(2^3\right)^n=8^n\)
=>\(3^{2n}>2^{3n}\)
b: \(199^{20}=\left(199^4\right)^5=1568239201^5\)
\(2003^{15}=\left(2003^3\right)^5=8036054027^5\)
mà \(1568239201< 8036054027\)
nên \(199^{20}< 2003^{15}\)
4: \(100< 5^{2x-1}< 5^6\)
mà \(25< 100< 125\)
nên \(125< 5^{2x-1}< 5^6\)
=>3<2x-1<6
=>4<2x<7
=>2<x<7/2
mà x nguyên
nên x=3
4 tháng 12 2021
Bài 1:
a: Tổng là:
(-19+19)+(-18+18)+...+20=20
b: Tổng là:
-18+(-17+17)+...+0=-18
YS
10 tháng 3 2016
A = 4 + (22 + 23 + 24 + ... + 220)
A - 4 = 22 + 23 + 24 + ... + 220
2(A - 4) = 23 + 24 + 25 + ... + 221
A - 4 = 2(A - 4) - (A - 4) = (23 + 24 + 25 + ... + 221) - (22 + 23 + 24 + ... + 220)
A - 4 = (23 - 23) + (24 - 24) + ... + (220 - 220) + (221 - 22)
A - 4 = 221 - 4
A = 221 - 4 + 4
A = 221
27 tháng 9 2017
\(A=1+2+2^2+...+2^{62}\)
\(\Rightarrow2A=2.\left(1+2+2^2+...+2^{62}\right)\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{63}\)
\(\Rightarrow2A-A=2+2^2+2^3+...+2^{63}-\left(1+2+2^2+...+2^{62}\right)\)
\(\Rightarrow A=2+2^2+2^3+...+2^{63}-1-2-2^2-...-2^{62}\)
\(\Rightarrow A=2^{63}-1\)
\(B=1+3+3^2+3^3+...+3^{20}\)
\(\Rightarrow3B=3+3^2+3^3+...+3^{21}\)
\(\Rightarrow3B-B=3+3^2+3^3+...+3^{21}-1-3-3^2-...3^{20}\)
\(\Rightarrow2B=3^{21}-1\)
\(\Rightarrow B=\frac{3^{21}-1}{2}\)
\(C=1+4+4^2+...+4^{49}\)
\(\Rightarrow4C=4+4^2+4^3+...+4^{50}\)
\(\Rightarrow4C-C=4+4^2+4^3+...+4^{50}-1-4-4^2-...-4^{49}\)
\(\Rightarrow3C=4^{50}-1\)
\(\Rightarrow C=\frac{4^{50}-1}{3}\)
NT
1
AH
Akai Haruma
Giáo viên
4 tháng 10 2024
Sẽ không tính được giá trị cụ thể của tổng A bạn nhé. Bạn xem lại đề.
