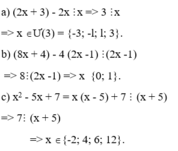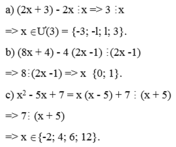Tìm x thuộc N biết : 5x chia hết cho (3+2x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
3
BT
13 tháng 11 2016
A=5x+6 =>2A=10x+12=5(2x+3)-3
B=2x+3
để a chia hết cho B thì 2A phải chia hết cho B
mà 5(2x+3) chia hết cho 2x+3 nên để 2A chia hết cho 3 thì -3 chi hất chi 2x+3
hay 2x+3 thuộc Ư (- 3) ta có U<-3>=(-1,1,3,-3 ) giải ra ta được x=-2=-1=-3=0
22 tháng 1 2016
3. Tìm n thuộc N để
a.27-5n chia hết cho n
do 5n chia hết cho n nên 27 phải chia hết cho n
n thuộc N nên n =1,3,9,27
và 5n< hoặc =27
suy ra n=1 hoặc 3
n=1 thỏa mãn
n=3 thỏa mãn
suy ra 2 nghiệm
KK
21 tháng 10 2018
a) ta có: 3x + 5 chia hết cho x + 1
=> 3x + 3 + 2 chia hết cho x + 1
3.(x+1) + 2 chia hết cho x + 1
mà 3.(x+1) chia hết cho x + 1
=> 2 chia hết cho x + 1
...
bn tự làm tiếp nha! phần b làm tương tự
IM
9 tháng 11 2016
a)
10 chia hết chp x+2
<=> \(x+2\inƯ_{10}\)
<=> \(x+2\in\left\{1;2;5;10\right\}\)
<=> \(x+2\in\left\{-1;0;3;8\right\}\)
Vậy \(x+2\in\left\{-1;0;3;8\right\}\)
b)
21 chia hết cho 2x + 5
\(\Leftrightarrow2x+5\in\left\{1;3;7;21\right\}\)
\(\Leftrightarrow2x+5\in\left\{-2;-1;1;8\right\}\)
Vậy ....
c) 18 chia hết cho x - 3
\(\Leftrightarrow x-3\in\left\{1;2;3;6;9;18\right\}\)
\(\Leftrightarrow x\in\left\{4;5;6;9;11;121\right\}\)
Vậy .........
d)
5x + 3 chia hết cho 3x + 2
<=> 3(5x + 3 ) - 5(3x+2) chia hết cho 3x + 2
<=> 15x + 9 - 15x - 10 chia hết cho 3x + 2
<=> - 1 chia hết cho 3x + 2
<=> 1 chia hết cho 3x + 2
<=> x = - 1
Vậy ....
NN
Tìm x thuộc N :
a) 2x + 1 chia hết cho x + 2
b) 5x + 2 chia hết cho x + 1
c) 3x + 1 chia hết cho 2x + 1
1
14 tháng 3 2020
a) Ta có: \(2x+1=\left(2x+4\right)-3=2.\left(x+2\right)-3\)
- Để \(2x+1⋮x+2\)\(\Leftrightarrow\)\(2.\left(x+2\right)-3⋮x+2\)mà \(2.\left(x+2\right)⋮x+2\)
\(\Rightarrow\)\(3⋮x+2\)\(\Rightarrow\)\(x+2\inƯ\left(3\right)\in\left\{\pm1;\pm3\right\}\)
- Ta có bảng giá trị:
| \(x+2\) | \(-1\) | \(1\) | \(-3\) | \(3\) |
| \(x\) | \(-3\) | \(-1\) | \(-5\) | \(1\) |
| \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) |
Vậy \(x\in\left\{-5,-3,-1,1\right\}\)
b) Ta có: \(5x+2=\left(5x+5\right)-3=5.\left(x+1\right)-3\)
- Để \(5x+2⋮x+1\)\(\Leftrightarrow\)\(5.\left(x+1\right)-3⋮x+1\)mà \(5.\left(x+1\right)⋮x+1\)
\(\Rightarrow\)\(3⋮x+1\)\(\Rightarrow\)\(x+1\inƯ\left(3\right)\in\left\{\pm1;\pm3\right\}\)
- Ta có bảng giá trị:
| \(x+1\) | \(-1\) | \(1\) | \(-3\) | \(3\) |
| \(x\) | \(-2\) | \(0\) | \(-4\) | \(2\) |
| \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) | \(\left(TM\right)\) |
Vậy \(x\in\left\{-4,-2,0,2\right\}\)
c) Để \(3x+1⋮2x+1\)\(\Leftrightarrow\)\(2.\left(3x+1\right)⋮2x+1\)
- Ta có: \(2.\left(3x+1\right)=6x+2=\left(6x+3\right)-1=3.\left(2x+1\right)-1\)
- Để \(2.\left(3x+1\right)⋮2x+1\)\(\Leftrightarrow\)\(3.\left(2x+1\right)-1⋮2x+1\)mà \(3.\left(2x+1\right)⋮2x+1\)
\(\Rightarrow\)\(1⋮2x+1\)\(\Rightarrow\)\(2x+1\inƯ\left(1\right)\in\left\{\pm1\right\}\)
+ \(2x+1=1\)\(\Leftrightarrow\)\(2x=0\)\(\Leftrightarrow\)\(x=0\left(TM\right)\)
+ \(2x+1=-1\)\(\Leftrightarrow\)\(2x=-2\)\(\Leftrightarrow\)\(x=-1\left(TM\right)\)
Vậy \(x\in\left\{-1,0\right\}\)
NT
0