Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ A=\left(4x^2+y^2\right)\left(4x^2-y^2\right)=16x^4-y^4\)
Đề sai, biểu thức A ko có m thì sao chứng minh?
\(2,\) Gọi 2 số nguyên lt là \(a;a+1\left(a\in Z\right)\)
Ta có \(a+1-a=1\) là số lẻ (đpcm)
\(3,P=9x^2+24x+16-10x-x^2+16=8x^2+14x+32\)
\(4,Q=x^2-4x+5=\left(x^2-4x+4\right)+1=\left(x-2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow x-2=0\Leftrightarrow x=2\)

\(a,P=5x\left(2-x\right)-\left(x+1\right)\left(x+9\right)\)
\(=10x-5x^2-\left(x^2+x+9x+9\right)\)
\(=10x-5x^2-x^2-x-9x-9\)
\(=\left(10x-x-9x\right)+\left(-5x^2-x^2\right)-9\)
\(=-6x^2-9\)
Ta thấy: \(x^2\ge0\forall x\)
\(\Rightarrow-6x^2\le0\forall x\)
\(\Rightarrow-6x^2-9\le-9< 0\forall x\)
hay \(P\) luôn nhận giá trị âm với mọi giá trị của biến \(x\).
\(b,Q=3x^2+x\left(x-4y\right)-2x\left(6-2y\right)+12x+1\)
\(=3x^2+x^2-4xy-12x+4xy+12x+1\)
\(=\left(3x^2+x^2\right)+\left(-4xy+4xy\right)+\left(-12x+12x\right)+1\)
\(=4x^2+1\)
Ta thấy: \(x^2\ge0\forall x\)
\(\Rightarrow4x^2\ge0\forall x\)
\(\Rightarrow4x^2+1\ge1>0\forall x\)
hay \(Q\) luôn nhận giá trị dương với mọi giá trị của biến \(x\) và \(y\).
#\(Toru\)

\(x^2-\sqrt{x}+\dfrac{1}{2}\)
\(=x^2-x+\dfrac{1}{4}+x-\sqrt{x}+\dfrac{1}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\left(\sqrt{x}-\dfrac{1}{2}\right)^2\ge0\)
Đẳng thức xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\\sqrt{x}-\dfrac{1}{2}=0\end{matrix}\right.\Rightarrow\) vô nghiệm
Vậy \(x^2-\sqrt{x}+\dfrac{1}{2}>0\forall x\ge0\)

Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
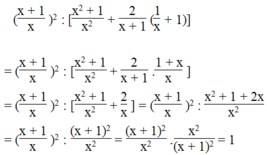
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.

a) Rút gọn E Þ đpcm.
b) Điều kiện xác định E là: x ≠ ± 1
Rút gọn F ta thu được F = 4 Þ đpcm

áp dụng BĐT | a | + | b | \(\ge\)| a + b | ta có :
| x - 2015 | + | 2016 - x | \(\ge\)| x - 2015 + 2016 - x | = 1
dấu " = " xảy ra khi ( x - 2015 ) . ( 2016 - x ) \(\ge\)0 hay 2015 \(\le\)x \(\le\)2016
Vậy ...

a) Ta có:
\(\begin{array}{l}P = 5{\rm{x}}\left( {2 - x} \right) - \left( {x + 1} \right)\left( {x + 9} \right)\\P = 5{\rm{x}}.2 - 5{\rm{x}}.x - x.x - x.9 - 1.x - 1.9\\P = 10{\rm{x}} - 5{{\rm{x}}^2} - {x^2} - 9{\rm{x}} - x - 9\\P = - \left( {6{{\rm{x}}^2} + 9} \right)\end{array}\)
Vì \(6{{\rm{x}}^2} \ge 0,\forall x \in \mathbb{R}\) nên \(6{{\rm{x}}^2} + 9 \ge 9,\forall x \in \mathbb{R}\) suy ra \( - \left( {6{{\rm{x}}^2} + 9} \right) \le - 9 < 0,\forall x \in \mathbb{R}\)
Vậy P luôn nhận giá trị âm với mọi giá trị của biến x.
b) Ta có:
\(\begin{array}{l}Q = 3{{\rm{x}}^2} + x\left( {x - 4y} \right) - 2{\rm{x}}\left( {6 - 2y} \right) + 12{\rm{x}} + 1\\Q = 3{{\rm{x}}^2} + x.x - x.4y - 2{\rm{x}}.6 - 2{\rm{x}}.\left( { - 2y} \right) + 12{\rm{x}} + 1\\Q = 3{{\rm{x}}^2} + {x^2} - 4{\rm{xy}} - 12{\rm{x}} + 4{\rm{xy + 12x + 1}}\\{\rm{Q = 4}}{{\rm{x}}^2} + 1\end{array}\)
Vì \({\rm{4}}{{\rm{x}}^2} \ge 0,\forall x \in \mathbb{R}\) nên \({\rm{4}}{{\rm{x}}^2} + 1 \ge 1 > 0,\forall x \in \mathbb{R}\)
Vậy Q luôn nhận giá trị dương với mọi giá trị của x, y.

`x^4+2x^2+1`
`=(x^2)^2 + 2.x^2 .1 + 1^2`
`=(x^2+1)^2 > 0 forall x`.
Đề là gì ạ