Tính tổng tất cả các giá trị nguyên của hàm số y=\(\dfrac{3sinx-cosx-4}{2sinx+cosx-3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
a.
\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge max\left(cosx\right)\)
\(\Leftrightarrow m\ge1\)
b.
\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)
\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)
\(\Leftrightarrow m\le-2\)
c.
\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
KC
1
T
1

31 tháng 7 2023
cot x=-2
=>cosx=-2*sinx
\(A=\dfrac{3sinx+2\cdot sinx}{2sinx+2\cdot sinx}=\dfrac{5}{4}\)




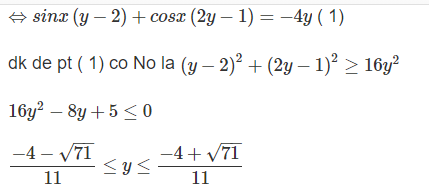


\(y=\dfrac{3sinx-cosx-4}{2sinx+cosx-3} \Leftrightarrow (2sinx+cosx-3)y=3sinx-cosx-4 \Leftrightarrow (3-2y)sinx+(y-1)cosx=4-3y \)
\(\Rightarrow (3-2y)^2+(y-1)^2 ≥ (4-3y)^2 \Leftrightarrow 5y^2−14y+10 ≥ 16−24y+9y^2 \Leftrightarrow 1 ≤ y ≤ \dfrac{3}{2}\)
Vậy hàm số không có giá trị nguyên.