trên cùng tia bx lấy điểm e và f sao cho BE=9cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
23 tháng 12 2019
a) Trên tia Bx có BE<BF ( 6cm<12cm)
=> E nằm giữa B,E
b) Vì E nằm giữa B,E( câu a)
=> BE+EF= BF
=> EF = 12 -6 =6 cm
Ta thấy EF = BE (=6cm) mà E nằm giữa 2 điểm B,F
=> E là trung điểm BF
23 tháng 12 2019
mk thấy câu trả lời của trang có vẻ là vẫn hơi vắn tắt , lúc mk cx lm như thế rồi nhưng cô bảo là phải diễn giải hẳn ra ko đc lm quá vắn tắt . Dòng thứ 5 của cậu phải là
Ta có: BE + EP = BF
Thay BF=12 cm ; BE = 6 cm
16 tháng 4 2021
(hình bạn tự vẽ nhé)
a) ta có:tam giác ABC=tam giác DCB (g.c.g)(1)
tam giác BED=tam giác DCB(g.c.g) (2)
Từ (1),(2)→tam giác ABC=tam giác BED (dfcm)
b) Tương tự câu a, ta chứng minh được ΔABC=ΔCDF
→AC = CF suy ra F là trung điểm của AF
c)Tương tự câu b, ta chứng minh được AB=BE,ED=DF
suy ra BF,CE là đường trung tuyến của ΔAEF
suy ra G là trọng tâm
CM
18 tháng 2 2018
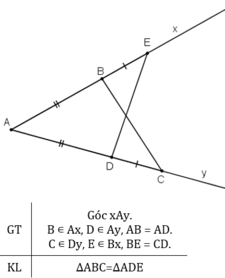
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.
Xét ΔABC và Δ ADE có:
AC = AE (cmt)
Góc A chung
AB = AD (gt)
⇒ ΔABC = ΔADE (c.g.c)
10 tháng 1 2024
1: Xét ΔMBE và ΔMCA có
MB=MC
\(\widehat{BME}=\widehat{CMA}\)(hai góc đối đỉnh)
ME=MA
Do đó: ΔMBE=ΔMCA
=>\(\widehat{MBE}=\widehat{MCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BE//AC
2: Sửa đề: Sao cho góc ABx nhận BC là tia phân giác
Xét ΔBAF có
BH là đường cao
BH là đường phân giác
Do đó: ΔBAF cân tại B
=>BA=BF
Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
=>AB=EC
mà AB=BF
nên BF=EC
3:
Ta có: ΔBAF cân tại B
mà BH là đường cao
nên H là trung điểm của AF
Xét ΔAFE có
H,M lần lượt là trung điểm của AF,AE
=>HM là đường trung bình của ΔAFE
=>HM//FE
=>BC//FE
Xét ΔKBC có FE//BC
nên \(\dfrac{KF}{FB}=\dfrac{KE}{EC}\)
mà FB=EC
nên KF=KE
Ta có: KF+FB=KB
KE+EC=KC
mà KF=KE và FB=EC
nên KB=KC
=>K nằm trên đường trung trực của BC(3)
Xét ΔBCE và ΔCBF có
BC chung
\(\widehat{BCE}=\widehat{CBF}\)(ΔKBC cân tại K)
CE=BF
Do đó: ΔBCE=ΔCBF
=>\(\widehat{IBC}=\widehat{ICB}\)
=>IB=IC
=>I nằm trên đường trung trực của BC(1)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(2)
Từ (1),(2),(3) suy ra K,I,M thẳng hàng
7 tháng 10 2021
Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC
13 tháng 12 2015
* Ta có AE=AB và BE=BA do đó AE=BF
* Ta có AB+BF=AF
AE+AB= EB
mà BF=AE . Do đó À=EB
TICK MÌNH NHA
l*l,c*c dqweferg54h45e565thhrhrwhthtr
rt
hưhưtrh
trh
ư
trư
h
rư
t