Nêu định nghĩa và các phương pháp tính tích phân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Loại 1: Đặt t=u(x)
- Loại 2: Đặt x=u(t)
Phương pháp đổi biến loại 1
Bài toán: Tính tích phân dạng: I=∫abf(u(x))(u(x))′dx
Phương pháp:
Đặt t=u(x)⇒dt=u′(x)dx
Đổi cận:
![]()
⇒I=∫u(a)u(b)f(t)dt
Ví dụ 1: Tính các tích phân sau:
a) I=∫01ex2+1xdx
Phân tích: Ta thấy có thể viết lại: I=∫01ex2+1xdx=∫01ex2+112.2xdx=12∫01ex2+1.2xdx
Trong đó 2x là đạo hàm của x2+1 nên ta có thể đặt t=x2+1.
Giải
Đặt t=x2+1⇒dt=2xdx
Đổi cận:
![]()
⇒I=12∫12etdt=12et∣∣∣21=12(e2−e)
b) J=∫01x3x2+1−−−−−√dx
Đặt t=x2+1−−−−−√⇒t2=x2+1⇒x2=t2−1⇒xdx=tdt
Đổi cận:
![]()
⇒J=∫01x2.x2+1−−−−−√.xdx=∫12√(t2−1).t.tdt=∫12√(t4−t2)dt
=(t55−t33)∣∣∣2–√1=22√+215
Một số bài tập áp dụng
1) J1 = ∫12xex2dx 2) J2 = ∫1e1+lnx√xdx
3) J3 = ∫01x3(x4−1)5dx 4) J4 = ∫024−x2−−−−−√.xdx
5) J5 = ∫0π/2cosx(1+sinx)4dx
Phương pháp đổi biến loại 2
Trong một số trường hợp đặt biệt, ta sẽ đổi biến bằng cách đặt x=u(t) để chuyển từ biến x về biến t. Một số trường hợp mà ta thường gặp có thể áp dụng phương pháp này:
1) Hàm số có chứa a2−x2−−−−−−√: đặt x=|a|sint với (−π2≤t≤π2) hoặc x=|a|cost với (0≤t≤π).
2) Hàm số có chứa x2−a2−−−−−−√: đặt x=|a|sint với (−π2≤t≤π2;t≠0) hoặc x=|a|cost với (0≤t≤π;t≠π2).
3) Hàm số có chứa a2+x2: đặt x=|a|tant với (−π2≤t≤π2) hoặc x=|a|cott với (0≤t≤π).
Ví dụ 3: Tình các tích phân sau:
a) I=∫024−x2−−−−−√dx
Giải
Đặt x=2sint (−π2≤t≤π2)
⇒dx=2costdt
Đổi cận:

⇒I=∫0π24−4sin2t−−−−−−−−√.2costdt=∫0π24(1−sin2t)−−−−−−−−−−√.2costdt
=∫0π24cos2t−−−−−√.2costdt=∫0π24cos2tdt=∫0π22(1+cos2t)dt
=2(t+12sin2t)∣∣∣π20=π
b) J=∫01x1+x2dx
Giải
Đặt x=tant⇒dx=1cos2tdt (−π2≤t≤π2)
Đổi cận:

⇒J=∫0π4tant1+tan2t(1+tan2t)dt=∫0π4tantdt=∫0π4sintcostdt
=−∫0π4(cost)′costdt=−ln(cost)∣∣∣π40=−ln2√2
Một số bài tập áp dụng:
1) ∫01dx1+x2 2) ∫02√2−x2−−−−−√dx 3) ∫2√2dxxx2−1√
4) ∫123√2dx1−x2√ 5) ∫13√9+3x2√dxx2
Định nghĩa : Cho f(x) là một hàm số liên tục trên đoạn [a; b] và giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b]. Khi đó hiệu F(b)−F(a) được gọi là tích phân từ a đến b của hàm số f(x).
Các phương pháp giải tích phân :
PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN

Cách đặt: Nhất lốc, nhì đa, tam lượng, tứ mũ (hàm logarit, hàm đa thức, hàm lượng giác, hàm mũ)

Nguyên hàm
Cho hàm số f(x) xác định trên K ( k là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K.
Phương pháp tính nguyên hàm
* Đổi biến số:
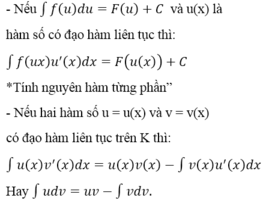

Phương pháp đổi biến số
Ta biết rằng nếu ∫f(x)dx=F(x)+C thì ∫f(t)dt=F(t)+C.
Từ đó ta có phương pháp để tìm nguyên hàm của những hàm số dạng g(x)=f(u(x))u′(x) bằng cách đặt t=u(x).
Nội dung phương pháp đổi biến số tính: ∫g(x)dx=∫f(u(x))u′(x)dx
Đặt t=u(x)⇒dt=u′(x)dx (lấy đạo hàm hai vế)
⇒∫g(x)dx=∫f(t)dt=F(t)+C
Ví dụ 1: Tìm nguyên hàm của hàm số f(x)=sin3xcosx
Phân tích: Ta thấy f(x)=sin3xcosx=(sinx)3(sinx)′ nên ta có thể đặt t=sinx.
Giải
t=sinx⇒dt=cosxdx
⇒∫sin3xcosxdx=∫t3dt=t44+C=sin4x4+C (C∈R)
Ví dụ 2: Tính ∫xx2+1−−−−−√dx
Phân tích: xx2+1−−−−−√=(x2+1)12122x=12(x2+1)12(x2+1)′
Giải
Đặt t=x2+1⇒dt=2xdx
∫xx2+1−−−−−√dx=∫(x2+1)12122xdx=12∫t12dt=t323+C
=(x2+1)323+C=(x2+1)x2+1√3+C (C∈R)
Lưu ý: Ta có thể giải ví dụ 2 như sau:
t=x2+1−−−−−√⇒t2=x2+1⇒2tdt=2xdx⇒tdt=xdx
⇒∫xx2+1−−−−−√dx=∫x2+1−−−−−√.xdx=∫t.tdt=∫t2dt
=t33+C=(x2+1√)33+C=(x2+1)x2+1√3+C
Nguyên hàm của một số hàm số hợp đơn giản
1) ∫kdx=kx+C
2) ∫(ax+b)αdx=1a(ax+b)α+1α+1+C(α≠1)
3) ∫dxax+b=1aln|ax+b|+C(x≠0)
4) ∫eax+bdx=1aeax+b+C
5) ∫cos(ax+b)dx=1asin(ax+b)+C
6) ∫sin(ax+b)dx=−1acos(ax+b)+C
7) ∫1cos2(ax+b)dx=1atan(ax+b)+C
8) ∫1sin2(ax+b)dx=−1acot(ax+b)+C . Định nghĩa
VÍ DỤ 1. Cho {F(x)=x3f(x)=3x2
VÍ DỤ 2. Cho {F(x)=cosxf(x)=−sinx
Ta thấy ở hai ví dụ trên đều có F’(x) = f(x). Ta gọi F(x) là một nguyên hàm của f(x). Vì với là một hằng số bất kỳ, ta có (F(x) + C)’ = F’(x) = f(x) nên nếu F(x) là nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x). Ta gọi F(x) + C, ( C là hằng số) là Họ nguyên hàm của f(x).
Ký hiệu: ∫f(x)dx=F(x)+C
VÍ DỤ:
∫x4dx=15x5+C;∫cosxdx=sinx+C

a, Phương pháp nêu định nghĩa, giải thích
+ Trong các câu văn trên người ta thường sử dụng nhiều từ "là. Sau từ đó người ta cung cấp tri thức về bản chất, đặc trưng của đối tượng.
+ Loại câu văn giải thích, định nghĩa trong thuyết minh có đặc điểm thường xuất hiện từ "là", đưa ra bản chất đối tượng.
b, Phương pháp liệt kê
Phương pháp liệt kê có tác dụng đưa ra hàng loạt số liệu, tính chất, đặc điểm của sự vật nào đó nhằm nhấn mạnh, khẳng định đối tượng cần thuyết minh làm rõ.
+ Đoạn Cây dừa Bình Định: liệt kê lợi ích từ tất cả các bộ phận của cây dừa đều hữu dụng.
+ Đoạn trích trong bài "Thông tin về ngày Trái Đất năm 2000 liệt kê hàng loạt tác hại của bao bì ni lông.
c, Phương pháp nêu ra ví dụ
- Nêu ví dụ là phương pháp thuyết minh có tính thuyết phục . Lấy dẫn chứng từ sách báo, đời sống để làm rõ điều mình trình bày.
+ Trong đoạn trích bài Ôn dịch, thuốc lá nêu ví dụ các nước phát triển xử phạt đối với người sử dụng thuốc lá.
d, Phương pháp dùng số liệu
- Phương pháp dùng số liệu là sử dụng những con số có tính định lượng để giải thích, minh họa, chứng minh cho một sự vật, hiện tượng nào đó.
e, Phương pháp so sánh
- Phương pháp so sánh trong văn thuyết minh là so sánh, đối chiếu một sự vật, hiện tượng nào đó trừu tượng, chưa thật gần gũi, còn mới mẻ với mọi người với những sự vật, hiện tượng thông thường, dễ gặp, dễ thấy.
f, Phương pháp phân loại, phân tích
- Áp dụng phương pháp phân loại, phân tích để làm rõ bản chất, đặc điểm của đối tượng, sự vật. Phương pháp này áp dụng với những đối tượng loại sự vật đa dạng, chia ra từng loại để trình bày.

Câu 3: Nếu không dùng phép lai phân tích, có thể sử dụng phương pháp tự thụ phấn ( giao phối gần ) để xác định một cơ thể mang tính trạng trội là đồng hợp hay dị hợp
- Nếu đời con đồng loạt về kiểu hình trội
=> cá thể mang tính trạng trội đem lai có KG đồng hợp tử
- Nếu đời con phân li kiểu hình : có trội, lặn
=> cá thể mang tính trạng trội đem lai có KG dị hợp tử

| Phân tích định tính | Phân tích định lượng |
| a/ Mục đích | |
| - Xác định nguyên tố nào có trong thành phần phân tử hợp chất hữu cơ | - Không những xác định được các nguyên tố nào có trong thành phần hợp chất hữu cơ mà còn xác định được thành phần phần trăm về khối lượng của các nguyên tố đó. |
| b/ Phương pháp tiến hành | |
| - Tìm C và H người ta nung hợp chất hữu cơ với CuO để chuyển C thành CO2, H thành H2O. | - Nung hợp chất hữu cơ với CuO. Hấp thụ nước bằng H2SO4 đặc, hấp thụ CO2 bằng KOH. Khối lượng tăng mỗi bình chính là khối lượng H2O và CO2 |
| - Chuyển N trong hợp chất hữu cơ thành NH3 | - Khối lượng khí N2 sinh ra thường được quy về đktc và tính |
| - Rồi nhận biết các hợp chất vô cơ đơn giản và quen thuộc trên. | - Từ đó tính được khối lượng C, H, N và phần trăm của chúng trong hợp chất |
| - Phầm trăm oxi được tính gián tiếp theo các chất đã tính được. |

a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c) 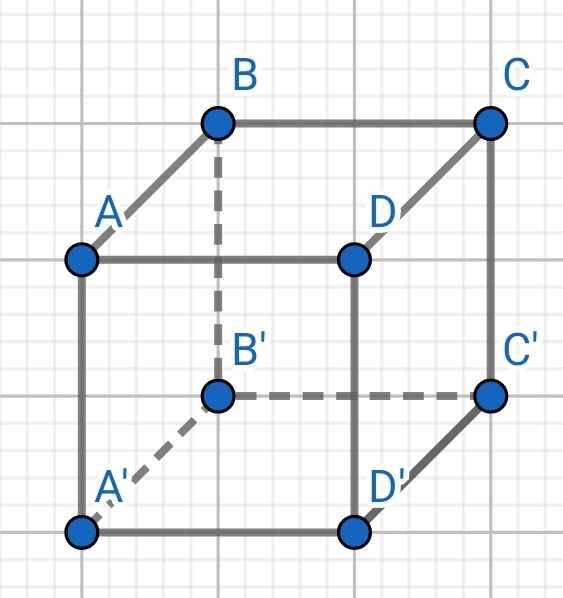
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3

a) Phân tích định tính
Mục đich: Xác định nguyên tố nào có trong thành phần phân tử chất hữu cơ
Phương pháp: Để xác định định tính C và H, nung chất hữu cơ với CuO để chuyển C thành CO2, H thành H2O, rồi phát hiện CO2 bằng nước vôi trong và H2O bằng CuSO4 khan. Còn với N thì chuyển thành NH3 rồi nhận ra bằng giấy quỳ ẩm
b) Phân tích định lượng
Mục đích: Xác định hàm lượng các nguyên tố trong phân tử chất hữu cơ Phương pháp: Nung a gam chất hữu cơ (C, H, O, N) với CuO dư. Hấp thụ hơi H2O và CO2 lần lượt bằng bình đựng H2SO4 đặc dư và KOH đặc dư. Độ tăng khối lượng mỗi bình chính là khối lượng H2O và CO2 tương ứng. Khí N2 thoát ra được xác định thể tích (ở đktc). Từ mH2O, mCO2 và VN2 rút ra mC, mH, mN và mO rồi suy ra hàm lượng của C, H, N và O.

Tham khảo:
Phương pháp phân tích các thế hệ lai:
+ Lai các cặp bố mẹ khác nhau về một hoặc một số cặp tính trạng thuần chủng tương phản.
+ Theo dõi sự di truyền riêng rẽ của từng cặp tính trạng qua các thế hệ.
+ Dùng toán thống kê để phân tích số liệu thu được
+ Rút ra quy luật di truyền các tính trạng
tham khảo :
Phương pháp phân tích các thế hệ lai:
+ Lai các cặp bố mẹ khác nhau về một hoặc một số cặp tính trạng thuần chủng tương phản.
+ Theo dõi sự di truyền riêng rẽ của từng cặp tính trạng qua các thế hệ.
+ Dùng toán thống kê để phân tích số liệu thu được
+ Rút ra quy luật di truyền các tính trạng
• Định nghĩa
Cho hàm số y = f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x)
• Phương pháp tính tích phân
a) Đổi biến số:
Định lí 1: Cho hàm số f(x) liên tục trên [a; b]. Giả sử hàm số x = φ(t) có đạo hàm liên tục trên đoạn [ α;β] sao cho φ(α) = a; φ(β) = βvà a ≤ φ(t) ≤ b với mọi t ∈ [α;β]. Khi đó:
b) Tích phân từng phần
Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì: