Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình vẽ:
A B C D
Giải:
Ta có: \(AB=\dfrac{BD}{2}\) ( \(A\) là trung điểm của \(BD\) )
Mà \(AB=AC\) ( Vì tam giác \(ABC\) cân tại \(A\) )
\(\Rightarrow AC=\dfrac{BD}{2}\)
Mà \(AC\) là đường trung tuyến của tam giác \(CBD\) ( \(A\) là trung điểm của\(BD \) ).
\(\Rightarrow\Delta CBD\) vuông tại \(C.\)
\(\Rightarrow\widehat{BCD}=90^o\)
Vì AC = AD
\(\Rightarrow\Delta ACD\) cân ại A
\(\Rightarrow\widehat{ACD}=\widehat{ADC}\) (1)
Vì \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\) (2)
\(\Delta BDC\) có :
\(\widehat{ABC}+\widehat{ACB}+\widehat{DCA}+\widehat{CDA}=180^0\)
Từ (1) và (2)
\(\Rightarrow\widehat{ABC}+\widehat{ADC}=\widehat{ACB}+\widehat{DCA}\)
\(\Rightarrow\left(\widehat{ACB}+\widehat{DCA}\right)\times2=180^0\)
\(\Rightarrow\widehat{ACB}+\widehat{DCA}=180^0\times\dfrac{1}{2}=90^0\)
\(\Rightarrow\widehat{BCD}=90^0\)
![]()
![]()
![]()

Ta có AB=AD nên CA là đường trung tuyến:
Suy ra tam giác BCD vuông tại C Suy ra góc BCD=90 độ
A B C D Ta có AB=AD nên CA là đường trung tuyến =>tam giác BCD vuông tại C => góc BCD =90 độ

A B C D
Có tam giác ABC cân tại A (gt)
=> AB = AC
Có A là trung điểm BD (gt)
=> AB = AD
=> AC = AD (= AB)
=> AC = \(\frac{1}{2}\)BD (= AB = AD)
Có A là trung điểm BD (gt)
=> CA là trung tuyến tam giác BDC
Mà CA = \(\frac{1}{2}\)BD (cmt)
=> tam giác BDC vuông tại C (đảo định lí trung tuyến ứng với cạnh huyền trong tam giác vuông)
=> góc BCD = 90o
Hình Giang vẽ rồi, tớ làm cách khác =)))
Tam giác ABC cân tại A \(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{ABC}=\widehat{ACB}\left(1\right)\end{cases}}\)
A là trung điểm của BD => AB=AD mà AB=AC => AD=AC
=> Tam giác CAD cân tại A => \(\widehat{ADC}=\widehat{ACD}\)(2)
Từ (1) và (2) => \(\widehat{ABC}+\widehat{ADC}=\widehat{ACB}+\widehat{ACD}=\widehat{BCD}\)
Tam giác BDC có: \(\widehat{ABC}+\widehat{ADC}+\widehat{BCD}=180^o\)(tổng 3 góc trong tam giác) =>\(\widehat{BCD}=\frac{180^o}{2}=90^o\)
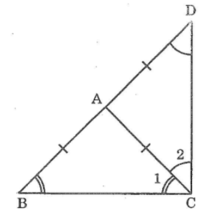
Ta có: ∆ABC cân tại A
⇒ AB = AC và ∠B = ∠C1 (tính chất tam giác cân) (1)
Lại có: AD = AB ( do A là trung điểm BD).
Suy ra: AD = AC do đó ∆ACD cân tại A
Nên ∠D =∠C2(tính chất tam giác cân) (2)
Mà ∠BCD =∠C1+ ∠C2 (3)
Từ (1); (2) và (3) suy ra: ∠BCD =∠B +∠D (4)
Trong ∆BCD, ta có:
∠BCD +∠B +∠D =180o (tổng 3 góc trong tam giác) (5)
từ (4) và (5) suy ra : 2 ∠BCD =180° hay∠BCD =90°