Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\overrightarrow{AB}=\left(-3;6\right)\)
\(\overrightarrow{AC}=\left(-3,5;7\right)\)
Vì \(\overrightarrow{AB}=\dfrac{7}{6}\overrightarrow{AC}\)
nên A,B,C thẳng hàng
a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right),\overrightarrow {AG} = \left( {2;1} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng
b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\)
Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\)
Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\)
\(\overrightarrow{AB}=\left(-4;-12\right)\)
\(\overrightarrow{AC}=\left(-1;-6\right)\)
Vì -4/-1<>-12/-6
nên A,B,C ko thẳng hàng
- Trên Hình 2, ba điểm thẳng hàng là: M, N, Q; ba điểm không thẳng hàng là M, N, P
- Trên Hình 3, ba điểm thẳng hàng là M, P, R
- Vẽ hình như sau:
Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: 
Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.
a) Ta có: \(\overrightarrow {AB} = \left( {3;2} \right),\overrightarrow {AC} = \left( { - 1; - 3} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Giả sử tọa độ điểm D là:\(D\left( {{x_D},{y_D}} \right)\)
Ta có: \(\overrightarrow {CD} = \left( {{x_D} - 0;{y_D} - \left( { - 2} \right)} \right) = \left( {{x_D};{y_D} + 2} \right)\)
Để tứ giác ABCD là hình thang có AB // CD và CD= 2AB thì \(\overrightarrow {CD} = 2\overrightarrow {AB} \)
Vậy nên \(\overrightarrow {CD} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2.3\\{y_D} + 2 = 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 6\\{y_D} = 2\end{array} \right.\)
Vậy tọa độ D là: \(D\left( {6;2} \right)\)
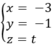
Phương pháp:
Sử dụng lý thuyết: Tứ diện OABC là tứ diện vuông tại O thì OH (với H là trục tâm tam giác ABC) chính là đường cao của tứ diện kẻ từ O.
Cách giải:
Dễ thấy các điểm A, B, C lần lượt thuộc các trục tọa độ nên OABC là tứ diện vuông tại O.
Do đó đường thẳng OH đi qua O và vuông góc mặt phẳng (ABC) hay nhận
Kiểm tra các đáp án ta loại được A, D.
Đáp án B: Kiểm tra điểm O thuộc đường thẳng (ứng với t = 1 ) nên đường thẳng ở đáp án B trung với OH.
Chọn B.