Cho tích phân với a, b, c là các số hữu tỉ. Tính giá trị của biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos4x=\dfrac{1}{2}+\dfrac{1}{2}cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow-cos4x=cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow cos\left(4x-\pi\right)=cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-\pi=2x-\dfrac{\pi}{2}+k2\pi\\4x-\pi=\dfrac{\pi}{2}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{3}\)
2.
\(\Leftrightarrow1-cos^2x+1-sin^24x=2\)
\(\Leftrightarrow cos^2x+sin^24x=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx=0\\sin4x=0\end{matrix}\right.\)
\(\Leftrightarrow cosx=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)

a) \(\left(sinx+cosx\right)^2=sin^2x+2sinxcosx+cos^2x\)\(=1+2sinxcosx\).
b) \(\left(sinx-cosx\right)^2=sin^2x-2sinxcosx+cos^2x\)\(=1-2sinxcosx\).
c) \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\).

\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)

\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)

1.
ĐKXĐ: \(x\ne k\pi\)
\(\Leftrightarrow\left(2cos2x-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\sinx=3>1\left(ktm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
2. Bạn kiểm tra lại đề, pt này về cơ bản ko giải được.
3.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{3\left(sinx+\dfrac{sinx}{cosx}\right)}{\dfrac{sinx}{cosx}-sinx}-2cosx=2\)
\(\Leftrightarrow\dfrac{3\left(1+cosx\right)}{1-cosx}+2\left(1+cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(\dfrac{3}{1-cosx}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\left(loại\right)\\cosx=\dfrac{5}{2}\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm

\(sin\left(x-\dfrac{\pi}{2}\right)+cos\left(x-\pi\right)+tan\left(\dfrac{5\pi}{2}-x\right)+tan\left(x-\dfrac{\pi}{2}\right)\)
\(=-sin\left(\dfrac{\pi}{2}-x\right)+cos\left(\pi-x\right)+tan\left(2\pi+\dfrac{\pi}{2}-x\right)-tan\left(\dfrac{\pi}{2}-x\right)\)
\(=-cosx-cosx+tan\left(\dfrac{\pi}{2}-x\right)-cotx\)
\(=-2cosx+cotx-cotx=-2cosx\)

a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
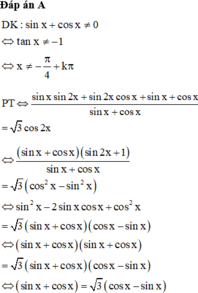
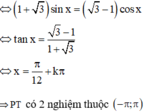
Đáp án D