Cho parabol (P) có phương trình . Tịnh tiến parabol (P) theo vectơ thu được đồ thị của hàm số nào dưới đây?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lấy M(x; y) thuộc (P); gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto v → ( - 2 ; - 1 ) thì:

Đáp án C

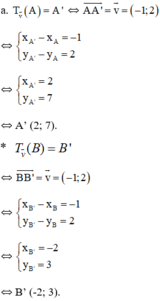
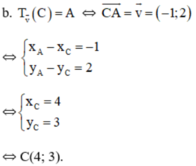
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

Tọa độ đỉnh của \(\left(P\right)\) là \(A\left(-3;-10\right)\)
Gọi A' là đỉnh của (P') thì A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=-3-3=-6\\y_{A'}=-1-10=-11\end{matrix}\right.\) \(\Rightarrow A'\left(-6;-11\right)\)

