cho tam giác ABC và ABD có AB=BC =3cm; AD=BD=2cm (C và D nắm khác phía với đối với AB). Chứng minh rắnggóc CAD= gócCBD
giúp mình với tối nay mình phải gửi cho cô rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 4 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)
hay AC=4(cm)
Vậy: AC=4cm
5 tháng 4 2021
b) Xét ΔABD vuông tại A và ΔEBC vuông tại E có
\(\widehat{ABD}=\widehat{EBC}\)(BE là tia phân giác của \(\widehat{ABC}\))
Do đó: ΔABD\(\sim\)ΔEBC(g-g)
CM
21 tháng 5 2017
Xét ΔCAD và ΔCBD, ta có:
AC = BC (= 3 cm)
AD = BD (= 2 cm)
CD cạnh chung
Suy ra: ΔCAD= ΔCBD(c.c.c)
Vậy ∠(CAD) =∠(CBD) ̂(hai góc tương ứng)
5 tháng 11 2016
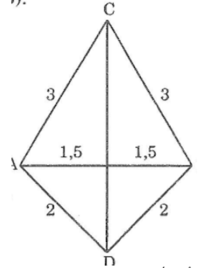
xét 2 tam giác ACD và BCD có AD=BD=2cm, AC=BC=3cm, CD chung
=> tg ACD= tg BCD (c.c.c) =>góc CAD= góc CBD
HN
5 tháng 3 2022
a,Xét tam giácCAD và tam giác CBD có:
CD:cạnh chumg
CA=CB
AD=BD
----->Tam giác CAD=tam giác CBD(c.c.c)
Vậy....
b,Có tam giác CAD=tam giác CBD(cmt)
-->Góc CAD=góc CBD(cặp góc tương ứng )
Vậy...
15 tháng 2 2018
tìm một số biết rằng số đó nhân với 3 thì được số lớn nhất có một chữ số.
25 tháng 3 2023
a: AB<AC<BC
=>góc C<gócB<góc A
b: Xét ΔABD và ΔEBD có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
c,d: ΔBAD=ΔBED
=>góc ADB=góc EDB và góc BAD=góc BED=90 độ
=>DB là phân giác của góc ADE và DE vuông góc BC
DM
4 tháng 2 2021
a, Có AB ^2 = 5^2=25
Có BC^2 +AC ^2= 4^2 +3^2=16+9=25
\(\Rightarrow\)AB^2 = AC^ 2+ BC^2 (=25)
\(\Rightarrow\)Tam giác ABC là tam giác vuông tại C ( Định lý pytago đảo)
\(\Rightarrow\)Góc ACB = 90 độ
b, Có góc BCD + góc ACB = 180 độ( 2 góc kề bù)
góc BCD + 90 độ = 180 độ
góc BCD = 90 độ
Xét tam giác ABC và BDC , có:
AC=CD ( vì cùng = 3cm)
góc ACB = góc BCD ( vì cùng = 90 độ)
BC là cạnh chung
\(\Rightarrow\)Tam giác ABC= Tam giác BCD (c.g.c)
\(\Rightarrow\) AB = BD (2 cạnh tương ứng)
Xét tam giác ABD, có:
AB = BD (chứng minh trên)
\(\Rightarrow\)Tam giác ABD cân tại B
Xét ΔCAD và ΔCBD, ta có:
AC = BC (= 3 cm)
AD = BD (= 2 cm)
CD cạnh chung
Suy ra: ΔCAD= ΔCBD(c.c.c)
Vậy ∠(CAD) =∠(CBD) ̂(hai góc tương ứng)