Gọi M là giá trị lớn nhất của hàm số xét trên đoạn [2;4], là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Xét hàm số ![]() hàm số liên tục trên R
hàm số liên tục trên R
Có ![]()
![]()
![]() đồng biến trên [2;4]
đồng biến trên [2;4]
![]()
Nên ![]()
Do đó ![]()
![]()
Ta có ![]()
![]()
![]()
Dấu bằng xảy ra 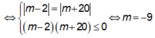
Vậy ![]()
![]()

\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)

Đáp án D
Xét hàm số ![]() .
.
![]() ;
;
![]()
![]()

Bảng biến thiên

Do ![]() nên
nên ![]() suy ra
suy ra ![]() .
.
Suy ra  .
.
Nếu ![]() thì
thì ![]() ,
, ![]()
![]()
![]()
![]() .
.
Nếu ![]() thì
thì ![]() ,
, ![]()
![]()
![]()
![]() .
.
Do đó ![]() hoặc
hoặc ![]() , do a nguyên và thuộc đoạn
, do a nguyên và thuộc đoạn ![]() nên
nên ![]() .
.

Ta có đạo hàm y’ = 3( x+ m) 2≥0 với mọi x.
=> Hàm số đồng biến trên đoạn [1; 2] nên hàm số đạt GTLN tại x = 2.
Khi đó; y( 2) = 8 khi và chỉ khi : ( 2+m) 3 = 8 hay m= 0
Chọn C.
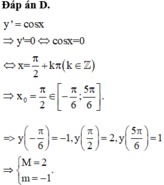
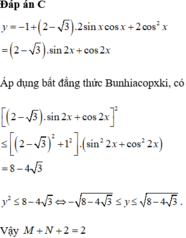
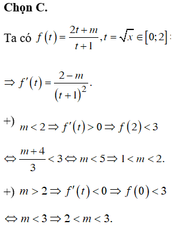
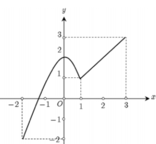
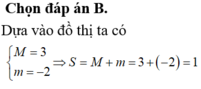
Đáp án là D