Phương trình mặt phẳng cách đều hai đường thẳng d 1 : x + 1 2 = y - 1 3 = z - 2 1 và d 2 : x - 2 1 = y + 2 5 = z - 2 là
A. - 11 x + 5 y + 7 z - 1 = 0
B. 11 x - 5 y - 7 z + 1 = 0
C. - 11 x + 5 y + 7 z + 1 = 0
D. - 11 x + 5 y + 7 z + 11 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
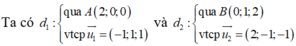
Mặt phẳng (P) song song và cách đều hai đường thẳng 
và 
nên:
(P) có một véc tơ pháp tuyến là 
suy ra (P):y-z+D=0
Và d (A, (P))=d (B, (P)) ó |D| = |D – 1| => D = 1/2
Vậy (P): 2y-2z+1=0.
\(\overrightarrow{u_{d1}}=\left(-1;1;1\right)\) ; \(\overrightarrow{u_{d2}}=\left(2;-1;-1\right)\)
\(\Rightarrow\left[\overrightarrow{u_{d1}};\overrightarrow{u_{d2}}\right]=\left(0;1;-1\right)\)
Do (P) song song \(d_1;d_2\Rightarrow\left(P\right)\) nhận \(\left(0;1;-1\right)\) là 1 vtpt
Phương trình (P) có dạng: \(y-z+c=0\)
Lấy \(A\left(2;0;0\right)\in d_1\) và \(B\left(0;1;2\right)\in d_2\)
Do (P) cách đều 2 đường thẳng \(\Rightarrow d\left(A;\left(P\right)\right)=d\left(B;\left(P\right)\right)\)
\(\Rightarrow\dfrac{\left|0-0+c\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\left|1-2+c\right|}{\sqrt{1^2+\left(-1\right)^2}}\Rightarrow\left|c\right|=\left|c-1\right|\)
\(\Rightarrow c=\dfrac{1}{2}\Rightarrow\) phương trình (P) có dạng:
\(y-z+\dfrac{1}{2}=0\)
Đáp án A
Vì hai đường thẳng d và d’ song song với nhau nên đường thẳng a cần tìm cũng song song với 2 đường thẳng nên a nhận u ⇀ =(3;1;-2) làm vecto chỉ phương.
Gọi A(2;-3;4) ∈ d ⇒ phương trình mặt phẳng (P) qua A vuông góc với d là: 3x+y-2z+5=0
Giao điểm H của (P) và d’ là H 4 7 ; - 15 7 ; - 16 7 . khi đó trung điểm của AH là I 9 7 ; - 18 7 ; 6 7
Thay tọa độ điểm I vào xem phương trình nào thỏa mãn.
Đáp án B
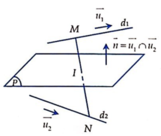
Đường thẳng d 1 có vecto chỉ phương u 1 → = 1 ; 0 ; - 2 và M ( 1 ; - 3 ; 2 ) ∈ d 1
Đường thẳng d 2 có vecto chỉ phương u 2 → 1 ; - 2 ; 3 và N - 3 ; 1 ; - 4 ∈ d 2
Trung điểm MN là I(-1;-1;-1); u 1 → ∧ u 2 → = - 4 ; - 5 ; - 2
Mặt phẳng (P) cách đều 2 đường thẳng d 1 , d 2 khi (P) qua I(-1;-1;-1) và có vecto pháp tuyến n → = n 1 → ∩ n 2 →
⇒ ( P ) : - 4 ( x + 1 ) - 5 ( y + 1 ) - 2 z ( z + 1 ) = 0 ⇔ 4 x + 5 y + 2 z + 11 = 0
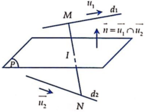
d 1 có vecto chỉ phương là u 1 → 2 ; 3 ; 1 tương ứng với d 2 có u 2 → 1 ; 5 ; - 2 . Gọi (P) là mặt phẳng cách đều d 1 và d 2 thì (P) có một vecto pháp tuyến là
Lấy điểm
Trung điểm đoạn AB là I 1 2 ; - 1 2 ; 1 . (P) đi qua I nên có phương trình là
Chọn C.