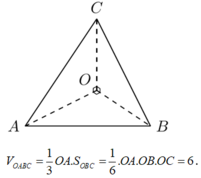
Khối chóp O.ABC có O B = O C = a , A O B ^ = A O C ^ = 45 ° , B O C ^ = 60 ° , O A = a 2 . Khi đó thể tích khối tứ diện O.ABC bằng:
A. a 2 12
B. a 3 2 12
C. a 3 3 12
D. a 3 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án là C.
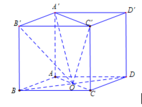
Ta có: V O . A , B , C , = 1 2 V O . A , B , C , D , ; V O . A , B , C , D , 1 3 V A B C D . A , B , C , D ,
V O . A , B , C , = 1 6 V A B C D . A , B , C , D , ⇒ V O . A , B , C , V A B C D . A , B , C , D = 1 6
Chọn B
Gọi A(a;0;0), B(0;b;0), C(0;0;c). Ta có phương trình mặt phẳng (P) là: 
Gọi H là hình chiếu của O lên (P). Ta có: d(O, (P)) = OH ≤ OM
Do đó max d(O, (P)) = OM khi và chỉ khi (P) qua M nhận 
làm VTPT.
Do đó (P) có phương trình:
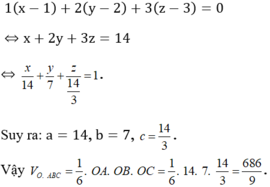
Đáp án B
Gọi H là hình chiếu của O trên (P) => d(O;(P)) = OH ≤ OM
Dấu bằng xảy ra khi và chỉ khi H ≡ M => n P → = (1;2;3) => (P): x + 2y + 3z - 14 = 0
Mặt phẳng (P) cắt các trục tọa độ lần lượt tại A(14;0;0); B(0;7;0); C(0;0; 14 3 )
Vậy thể tích khối chóp OABC là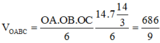 
Đáp án B
Gọi H là hình chiếu của O trên (P)
Dấu bằng xảy ra khi và chỉ khi
Mặt phẳng (P) cắt các trục tọa độ lần lượt tại
Vậy thể tích khối chóp OABC là
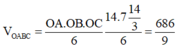
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\( \Rightarrow R = \dfrac{a}{{2\sin A}};\;\;b = \dfrac{{a.\sin B}}{{\sin A}}\)
Mà \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\)
\( \Rightarrow R = \dfrac{{10}}{{2\sin {{45}^o}}} = 5\sqrt 2 ;\;\;b = \dfrac{{a.\sin {{70}^o}}}{{\sin {{45}^o}}} \approx 13,29\)
Mặt khác: \(\widehat A = {45^o},\widehat B = {70^o} \Rightarrow \widehat C = {65^o}\)
Từ định lí sin ta suy ra: \(c = \dfrac{{a.\sin C}}{{\sin A}} = \dfrac{{10.\sin {{65}^o}}}{{\sin {{45}^o}}} \approx 12,82.\)
Vậy \(R = 5\sqrt 2 ;\;\;b \approx 13,29\); \(c \approx 12,82.\)
Ta có: \(\overrightarrow a .\overrightarrow b = 1.( - 2) + ( - 1).0 = - 2 \ne 0\).
Lại có: \(|\overrightarrow a | = \sqrt {{1^2} + {{( - 1)}^2}} = \sqrt 2 ;\;|\overrightarrow b | = \sqrt {{{( - 2)}^2} + {0^2}} = 2.\)
\( \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.\;|\overrightarrow b |}} = \frac{{ - 2}}{{\sqrt 2 .2}} = \frac{{ - \sqrt 2 }}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {135^o}\)
Chọn C
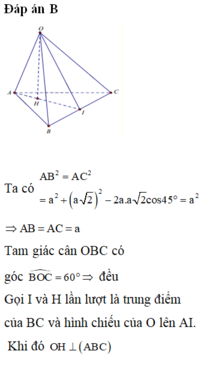
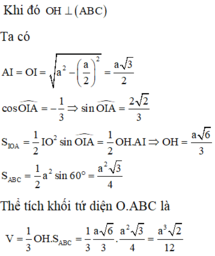
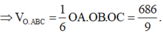
Đáp án B
Ta có A B 2 = A C 2 = a 2 + a 2 2 − 2 a . a 2 c o s 45 ° = a 2
⇒ A B = A C = a
Tam giác cân OBC có góc B O C ^ = 60 ° ⇒ đều
Gọi I và H lần lượt là trung điểm của BC và hình chiếu của O lên AI. Khi đó O H ⊥ A B C
Ta có
A I = O I = a 2 − a 2 2 = a 3 2 cos O I A ^ = − 1 3 ⇒ sin O I A ^ = 2 2 3 S I O A = 1 2 I O 2 sin O I A ^ = 1 2 O H . A I ⇒ O H = a 6 3 S A B C = 1 2 a 2 sin 60 ° = a 2 3 4
Thể tích khối tứ diện O.ABC là V = 1 3 O H . S A B C = 1 3 a 6 3 . a 2 3 4 = a 3 2 12