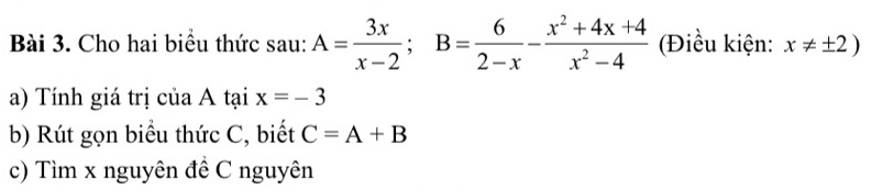vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn
vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.
Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)
\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp
\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp
Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)
I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)
\(\Rightarrow\) Tọa độ I thỏa mãn:
\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)
\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)
\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)
Phương trình (S):
\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)

Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)

a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)

a: Xét ΔBAE vuông tại A và ΔBIE vuông tại I có
BE chung
\(\widehat{ABE}=\widehat{IBE}\)
Do đó: ΔBAE=ΔBIE
Suy ra: BA=BI
hay ΔBIA cân tại B
b: Ta có: ΔBAE=ΔBIE
nên EA=EI
hay E nằm trên đường trung trực của AI(1)
Ta có: BA=BI
nên B nằm trên đường trung trực của AI(2)
Từ (1) và (2) suy ra BE là đường trung trực của AI
hay BE\(\perp\)AI
c: Xét ΔAEK vuông tại A và ΔIEC vuông tại I có
EA=EI
\(\widehat{AEK}=\widehat{IEC}\)
Do đó:ΔAEK=ΔIEC
Suy ra: AK=IC
Ta có: BA+AK=BK
BI+IC=BC
mà BA=BI
và AK=IC
nên BK=BC
hay ΔBKC cân tại B
d: Xét ΔBKC có BA/BK=BI/BC
nên AI//KC

a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot NP=MN^2\left(1\right)\)
Xét ΔMNK vuông tại M có MQ là đường cao
nên \(NQ\cdot NK=MN^2\left(2\right)\)
Từ (1) và (2) suy ra \(NH\cdot NP=NQ\cdot NK\)