Mình đang cần gấp ạ
Từ điểm A ởngoài (O;R) với OA = R√2, gọi H là trung điểm OA. Qua H vẽdây cung BC vuông góc OA. Chứng minh AB, AC là tiếp tuyến của (O)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
14 tháng 3 2023
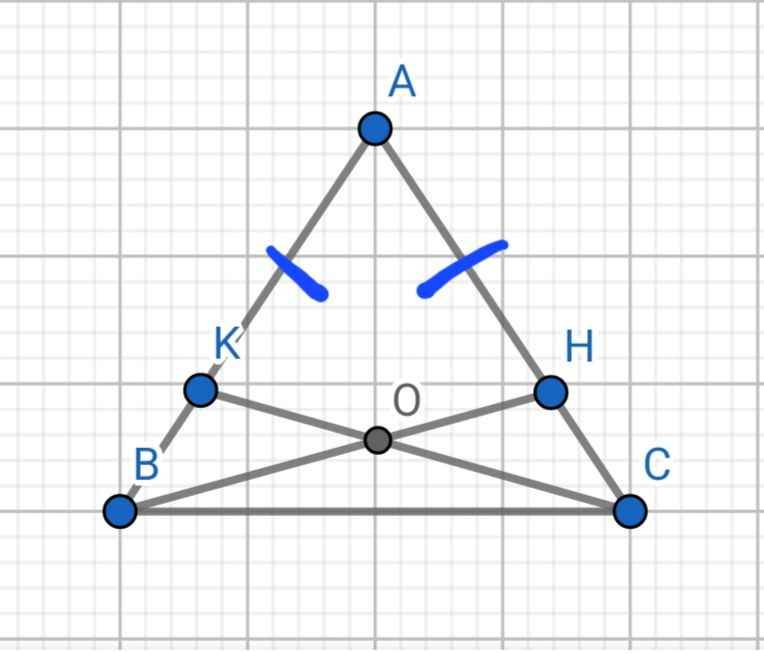
Do ∆ABC cân tại A
⇒ AB = AC và ∠ABC = ∠ACB
AK = AH
⇒ BK = CH
Xét ∆BHC và ∆CKB có:
CH = BK (cmt)
∠BCH = ∠CBK (∠ACB = ∠ABC)
BC chung
⇒ ∆BHC = ∆CKB (c-g-c)
⇒ ∠HBC = ∠KCB (hai góc tương ứng)
∠OBC = ∠OCB
∆OBC có ∠OBC = ∠OCB
⇒ ∆OBC cân tại O
14 tháng 3 2023
Vì tam giác ABC cân tại A, nên ta có AB = AC.
Với AK = AH và AB = AC, ta có tam giác AKH cân tại A.
Gọi M là trung điểm của KH, ta có AM song song với BC và AM = 1/2 BC.
Ta thấy rằng tam giác BOM và COM đều có cạnh ON (với N là trung điểm BC), BM = MC và góc BOM = 180° - góc COM.
Như vậy, tam giác BOC cân tại O vì OB = OC (cùng là đường trung bình trong tam giác đều BOC) và góc BOC = 2 × góc BOM = 2× (90° – 1/2 × góc MBC) = 180° – góc MBC = góc BOC (vì tam giác BOC cân tại O).
ND
1
SV
Sinh Viên NEU
CTVVIP
1 tháng 11 2023
10 C
11 A
12 D
13 B
14 D
15 D
16 B
17 A
18 C
19 D
20 B
21 B
22 C
23 A
24 A
25 C
TD
14
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
Tất cả k dưới đây đều là \(k\in Z\)
6.
\(\Leftrightarrow\sqrt{3}cot\left(3x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=cot\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow3x=\dfrac{2\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{9}+\dfrac{k\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
7.
\(\Leftrightarrow\sqrt{3}tan\left(3x-15^0\right)=-1\)
\(\Leftrightarrow tan\left(3x-15^0\right)=-\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow tan\left(3x-15^0\right)=tan\left(-30^0\right)\)
\(\Leftrightarrow3x-15^0=-30^0+k180^0\)
\(\Leftrightarrow3x=-15^0+k180^0\)
\(\Leftrightarrow x=-3^0+k60^0\)