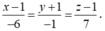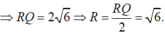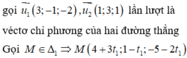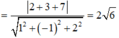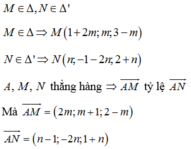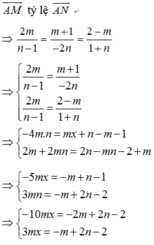Trong không gian Oxyz, cho đường thẳng . Có tất cả bao nhiêu giá trị thực của m để phương trình là phương trình của một mặt cầu (S) sao cho có duy nhất một mặt phẳng chứa Δ và cắt (S) theo giao tuyến là một đường tròn có bán kính bằng 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


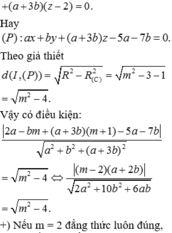
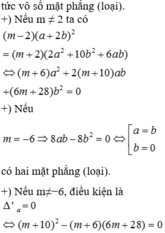


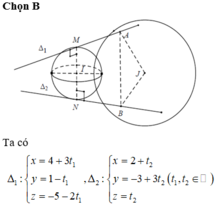
Đường thẳng d1 qua điểm ![]() đường thẳng d2 qua điểm
đường thẳng d2 qua điểm ![]() Ta có
Ta có ![]() chéo nhau hoặc cắt nhau. Để d1, d2 cắt nhau điều kiện là
chéo nhau hoặc cắt nhau. Để d1, d2 cắt nhau điều kiện là
![]()
![]()
![]() (luôn đúng).
(luôn đúng).
Vậy với mọi m hai đường thẳng đã cho luôn cắt nhau.
Chọn đáp án D.

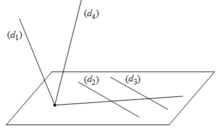
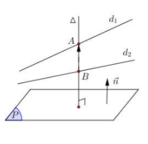
Hai đường thẳng d 1 , d 3 song song và nằm trong mặt phẳng 3y + z -6 =0.
Hai đường thẳng d 2 , d 4 phân biệt cùng cắt mặt phẳng 3y + z -6 =0. tại điểm A(4;2;0).
Qua A có vô số đường thẳng cắt Hai đường thẳng d 1 , d 3 . Vậy có vô số đương thẳng cắt bốn đường thẳng đã cho.
Đáp án B

Chọn D
Đường thẳng d₁ đi qua điểm M₁ = (3;-1;-1) và có một véctơ chỉ phương là ![]()
Đường thẳng d₂ đi qua điểm M₂ = (0;0;1) và có một véctơ chỉ phương là ![]()
Do ![]() và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
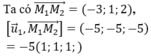
Gọi (α) là mặt phẳng chứa d₁ và d₂ khi đó (α) có một véctơ pháp tuyến là ![]() . Phương trình mặt phẳng (α) là x+y+z-1=0.
. Phương trình mặt phẳng (α) là x+y+z-1=0.
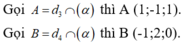
Do ![]() không cùng phương với
không cùng phương với ![]() nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.
nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.

Chọn D
Đường thẳng d1 đi qua điểm M1 (3; -1; -1) và có một véctơ chỉ phương là ![]()
Đường thẳng d2 đi qua điểm M2 (0; 0; 1) và có một véctơ chỉ phương là ![]()
Do ![]() và M1 ∉ d1 nên hai đường thẳng d1 và d2 song song với nhau.
và M1 ∉ d1 nên hai đường thẳng d1 và d2 song song với nhau.
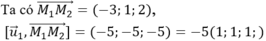
Gọi (α) là mặt phẳng chứa d1 và d2 khi đó (α) có một véctơ pháp tuyến là ![]()
Phương trình mặt phẳng (α) là x + y + z -1 = 0
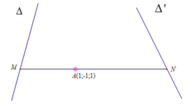
Gọi A = d3 ∩ (α) thì A (1; -1; 1)
Gọi B = d4 ∩ (α) thì B (-1; 2; 0)
Do ![]() không cùng phương với
không cùng phương với ![]() nên đường thẳng AB cắt hai đường thẳng d1 và d2.
nên đường thẳng AB cắt hai đường thẳng d1 và d2.

Chọn C
Gọi d là đường thẳng cần tìm.

Đường thẳng cần tìm qua A và nhận ![]() là véc tơ chỉ phương nên có phương trình:
là véc tơ chỉ phương nên có phương trình: