Cho hàm số . Khi hàm số có cực trị, giá trị của bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

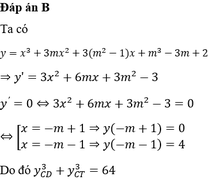

Để hàm số ![]() có đúng 3 cực trị thì hàm số
có đúng 3 cực trị thì hàm số ![]() có 2 cực trị trái dấu.
có 2 cực trị trái dấu.
Trước hết cần điều kiện m-1≠0
⇔m≠1
Ta có ![]()
Để hàm số
![]() có 2 cực trị trái dấu thì phương trình y'=0 có 2 nghiệm trái dấu
có 2 cực trị trái dấu thì phương trình y'=0 có 2 nghiệm trái dấu ![]()
Kết hợp điều kiện ![]()
Khi m=1 thì hàm số trở thành ![]() có 1 cực trị Khi đó hàm số
có 1 cực trị Khi đó hàm số ![]() có đúng 3 điểm cực trị.
có đúng 3 điểm cực trị.
Vậy m∈-2;-1;0;1
Chọn C

- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)

\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)

Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

+ Ta có đạo hàm y’ = 3x2- 12x+ 3( m+ 2)
Phương trình y’ = 0 khi 3x2- 12x+ 3( m+ 2) = 0
+ Hàm số có 2 điểm cực trị x1; x2 ⇔ Δ’ > 0 ⇔ m < 2
+ Chia y cho y’ ta được :y= 1/3.y’( x-2) + (m-2) (2x+ 1)
Tọa độ 2 điểm cực trị tương ứng : A( x1 ; ( m-2) ( 2x1+ 1) ) và B( x2 ; ( m-2) ( 2x2+ 1) )
+ ta có ; y1.y2= ( m-2) 2( 4x1x2+ 2( x1+ x2) + 1)
Với 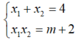 nên: y1y2= ( m-2) 2( 4m+ 17)
nên: y1y2= ( m-2) 2( 4m+ 17)
Hai cực trị cùng dấu khi và chỉ khi y1.y2> 0 hay ( m-2) 2( 4m+ 17) > 0
⇔ m > - 17 4 m ≠ 2
Kết hợp điều kiện ta được : -17/4< m< 2; mà m nguyên nên m= -4; -3; ...0; 1
Có tất cả 6 giá trị nguyên của m thỏa mãn đầu bài.
Chọn C.


