Cho hàm số f ( x ) = x 2 - 4 x - 2 n ế u x ≢ 2 m 3 + 3 m n ế u x = 2 . Tìm m để hàm số liên tục tại x 0 = 2
A. m = 0 hoặc m = 1
B. m = 1 hoặc m = -4
C. m = -4 hoặc m = 1
D. m = 0 hoặc m = -4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(TXĐ=D=R\)
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)
a, đk : \(\hept{\begin{cases}2-x\ge0\\x+2\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le2\\x\ge-2\end{cases}}\Leftrightarrow-2\le x\le2\)
b, Gỉa sử f(a) = f(-a)
\(\sqrt{2-a}+\sqrt{a+2}=\sqrt{2-\left(-a\right)}+\sqrt{-a+2}\)*đúng*
Vậy ta có đpcm
c, Ta có : \(y^2=2-x+x+2+2\sqrt{4-x^2}=4+2\sqrt{4-x^2}\)
Do \(2\sqrt{4-x^2}>0\Rightarrow4+2\sqrt{4-x^2}>4\)với -2 =< x =< 2
Vậy y^2 > 4

Bài 1:
Để \(F\left(x\right)=G\left(x\right)\) thì \(3x^2-8x+4=3x+4\)
\(\Leftrightarrow3x^2-11x=0\)
\(\Leftrightarrow x\left(3x-11\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{11}{3}\end{matrix}\right.\)

1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

Chọn B
Ta có
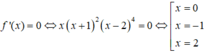
Bảng biến thiên
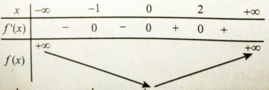
Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại x = 0. Vậy hàm số có một cực trị

Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.

Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.