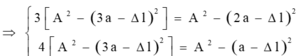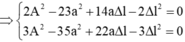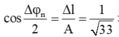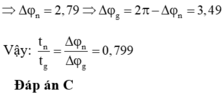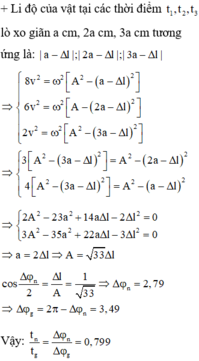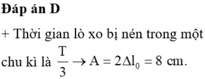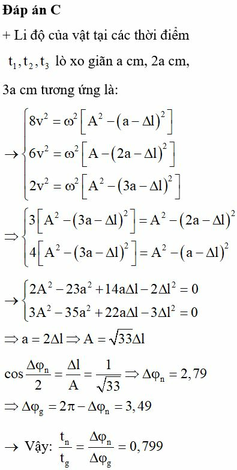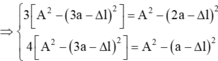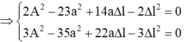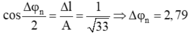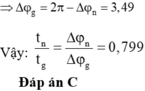Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, gốc O ở VTCB. Tại các thời điểm lò xo dãn a (cm); 2a (cm); 3a (cm) tương ứng với tốc độ của vật là và .Tỉ số giữa thời gian lò xo nén và lò xo dãn trong 1 chu kỳ là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\omega=\sqrt{\dfrac{g}{\Delta l}}\Rightarrow\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\pi\right)^2}=\dfrac{1}{100}\left(m\right)=1\left(cm\right)\)
Đưa con lắc đến vị trí lò xo ko biến dạng, tức là lúc này vật có li độ là: \(x=\Delta l=1cm\)
\(\Rightarrow A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{1+\dfrac{\left(10\pi\sqrt{3}\right)^2}{\left(10\pi\right)^2}}=\sqrt{1+3}=2\left(cm\right)\)
Ta đã biết lực đàn hồi luôn có chiều chống lại tác nhân gây biến dạng, tức là nếu lò xo dãn, thì lực đàn hồi có xu hướng kéo lại, tức hướng lên; nếu lò xo nén, thì lực đàn hồi có xu hướng đẩy ra, tức hướng xuống
Còn lực kéo về là tổng hợp các lực tác dụng lên vật, có biểu thức là \(\overrightarrow{F}=m.\overrightarrow{a}\) nên lực kéo về sẽ luôn cùng chiều với gia tốc a, tức là luôn hướng về VTCB.
Biểu diễn 2 lực đó trên giấy, ta thấy chúng ngược chiều nhau khi vật đi từ \(\Delta l\rightarrow VTCB\) và \(VTCB\rightarrow\Delta l\)
Sử dụng đường tròn lượng giác, ta thấy trong một chu kỳ, tổng góc mà nó quay được khi đi từ \(\Delta l\rightarrow VTCB\) và \(VTCB\rightarrow\Delta l\) là:
\(\varphi=2arc\sin\left(\dfrac{\Delta l}{A}\right)=2arc\sin\left(\dfrac{1}{2}\right)=2.\dfrac{\pi}{6}=\dfrac{\pi}{3}\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{\pi}{3.10\pi}=\dfrac{1}{30}\left(s\right)\)

Đáp án C
Li độ của vật tại các thời điểm t 1 , t 2 , t 3 lò xo giãn a cm, 2a cm, 3a cm tương ứng là:
![]()
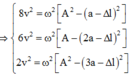
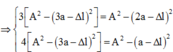
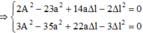
![]()
![]()
![]()
![]()
Vậy: