Câu 3: ( 3 điểm) Cho đoạn thẳng AB = 3 cm.
Nêu cách vẽ, ký hiệu đường trung trực của đoạn thẳng AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



- Vẽ đoạn thẳng AB = 24mm
- Vẽ trung điểm I cuả AB
Vì I là trung điểm của AB nên IA = IB = AB/2 = 12 (mm)
Đặt thước thẳng trùng với đường thẳng AB sao cho vạch 0 trùng với điểm A , vạch 12 cho ta vị trí điểm I.
- Vẽ đường thẳng d đi qua I và d⊥ AB
Đặt êke sao cho một cạnh góc vuông của êke trùng với đường thẳng AB, đỉnh góc vuông của êke trùng với I, vẽ đường thẳng đi qua cạnh góc vuông còn lại của êke ta được đường thẳng d.
Khi đó d là trung trực của AB.
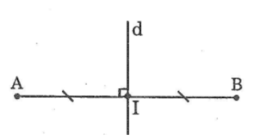

Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.

A B I d
Chia đoạn thẳng thành 2 phần bằng nhau , Chấm một điểm I vào trung điểm của đoạn thẳng đó .
Đưa một cạnh của eke khớp với đoạn AI hoặc BI
Góc vuông của eke khớp vs điểm I(trung điểm)
Kẻ một đường thẳng qua I theo cạnh còn lại của eke .

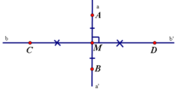
a,a, Vì OC⊥d,OD⊥d⇒C,O,DOC⊥d,OD⊥d⇒C,O,D thẳng hàng
b,b, Vì OC=2cmOC=2cm , OD=1cmOD=1cm ⇒ OCOC ≠≠ ODOD ⇒D⇒D không phải trung điểm của CDCD
Mà D∈dD∈d ⇒d⇒d không phải đường trung trực của CD


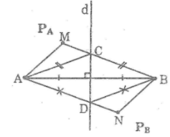
Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.
Ta có: NA = ND + DA
mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có:
NB < ND + DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB

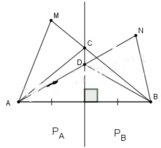
Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.
Ta có: MB = MC + CB
mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB